
【题目】一扇窗户如图1所示,窗框和窗扇用“滑块铰链”连接.如图2是图1中“滑块铰链”的平面示意图,滑轨MN安装在窗框上,托悬臂DE安装在窗扇上,支点4处装有滑块,滑块可以左右滑动,支点B,C,D在一条直线上,延长DE交MN于点F.已知AC=DE=20cm,AE=CD=10cm,BD=40cm.

(1)当∠CAB=35 时,求窗扇与窗框的夹角∠DFB的度数.
(2)当窗扇关闭时,图中点E,A,D,C,B都在滑轨MN上.求此时点A与点B之间的距离.
(3)在(2)的前提下,将窗户推开至四边形ACDE为矩形时,求点A处的滑块移动的距离.
【答案】(1)35°;(2)50,(3)![]()
【解析】(1)根据两组对边分别相等的四边形是平行四边形,可证明四边形AEDC是平行四边形,再根据平行四边形的性质,证明DF∥AC,从而可求出结果;
(2)将图形抽象出来。先求出BC的长,再根据AB=AC+CB,就可求出答案;
(3)根据题意画出图形,利用勾股定理求出A1B的长,再利用A1A=AB-A1B,即可解答.
(1)解:∵AC=DE,AE=CD
∴四边形AEDC是平行四边形
∴DF∥AC
∴∠DFB=∠CAB=35°
(2)解:如图

∵BC=BD-CD=40-10=30
∴AB=AC+CB=20+30=50
(3)解:如图,窗户户推开至四边形A1CDE为矩形时

在Rt△A1CB中,A1B=![]()
∴点A处的滑块移动的距离A1A=AB-A1B=50-![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=AD=5,BC=CD且BC>AB,BD=8.给出以下判断:
①AC垂直平分BD;
②四边形ABCD的面积S=ACBD;
③顺次连接四边形ABCD的四边中点得到的四边形可能是正方形;
④当A,B,C,D四点在同一个圆上时,该圆的半径为![]() ;
;
⑤将△ABD沿直线BD对折,点A落在点E处,连接BE并延长交CD于点F,当BF⊥CD时,点F到直线AB的距离为![]() .
.
其中正确的是_____.(写出所有正确判断的序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,对角线AC,BD交于点0,过点0的直线分别交边AD,BC于点E,F,EF=6.则AE2+BF2的值为( )
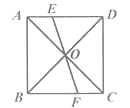
A. 9 B. 16 C. 18 D. 36
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若点P为四边形ABCD内一点,且满足∠APB+∠CPD=180°, 则称点P为四边形ABCD的一个“互补点”.
(1)如图1,点P为四边形ABCD的一个“互补点”,∠APD=63°,求∠BPC的度数.

(2)如图2,点P是菱形ABCD对角线上的任意一点.求证:点P为菱形ABCD的一个“互补点”.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“十一”黄金周期间,某市在![]() 天中外出旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)
天中外出旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)
日期 |
|
|
|
|
|
|
|
人数变化(万人) |
|
|
|
|
|
|
|
(1)若![]() 月
月![]() 日外出旅游人数为
日外出旅游人数为![]() ,那么
,那么![]() 月
月![]() 日外出旅游的人数是多少?
日外出旅游的人数是多少?
(2)请判断七天内外出旅游人数最多的是哪天?最少的是哪天?它们相差多少?
(3)如果最多一天有出游人数![]() 万人,那么若
万人,那么若![]() 月
月![]() 日外出旅游的有多少人?
日外出旅游的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=![]() +bx+c图像的一部分,图像过点A(-3,0),对称轴是直线x=-1,给出四个结论,其中正确结论的个数为( )
+bx+c图像的一部分,图像过点A(-3,0),对称轴是直线x=-1,给出四个结论,其中正确结论的个数为( )

①c>0; ② 2a-b=0; ③![]() <0. ④若点B(-
<0. ④若点B(-![]() ,
,![]() )、C(-
)、C(-![]() ,
,![]() )在图像上,则
)在图像上,则![]() <
<![]()
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
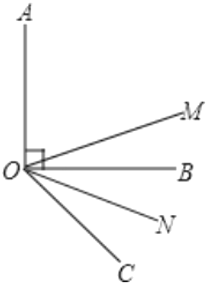
【题目】如图,已知![]() 与
与![]() 互为余角,且
互为余角,且![]() 平分
平分![]() 平分
平分![]() .
.
(1)求![]() 的度数;
的度数;
(2)如果已知![]() ,其他条件不变,则
,其他条件不变,则![]() _______度;如果已知
_______度;如果已知![]() ,其他条件不变,则
,其他条件不变,则![]() _______度;
_______度;
(3)从以上求![]() 的过程中,你得出的结论是__________.
的过程中,你得出的结论是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】建设银行的某储蓄员小张在办理业务时,约定存入为正,取出为负. 2019年10月29日,他先后办理了七笔业务: +2000元、-800元、+400元、-800元、+1400元、-1700元、-200元.
(1)若他早上领取备用金4000元,那么下班时应交回银行_________元钱.
(2)请判断在这七次办理业务中,小张在第_______次业务办理后手中现金最多,第_________次业务办理后手中现金最少.
(3)若每办一件业务,银行发给业务量的0.2%作为奖励,小张这天应得奖金多少元?
(4)若记小张第一次办理业务前的现金为0点,用折线统计图表示这7次业务办理中小张手中现金的变化情况.
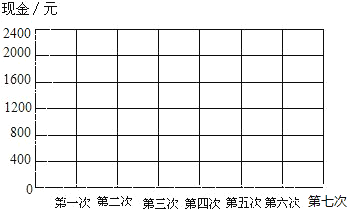
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请把下列证明过程补充完整.已知:如图,B、C、E三点在同一直线上,A、F、E三点在同一直线上,∠1=∠2=∠E,∠3=∠4.求证:AB∥CD.
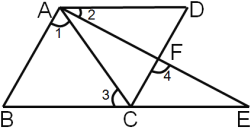
证明:∵∠2=∠E(已知)
∴ ∥BC( )
∴∠3=∠ ( )
∵∠3=∠4(已知)
∴∠4=∠ ( )
∵∠1=∠2(已知)
∴∠1+∠CAF=∠2+∠CAF ,即∠BAF=∠
∴∠4=∠ (等量代换)
∴ ( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com