
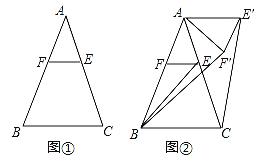
【题目】已知,△ABC中,AB=AC,点E是边AC上一点,过点E作EF∥BC交AB于点F
(1)如图①,求证:AE=AF;
(2)如图②,将△AEF绕点A逆时针旋转α(0°<α<144°)得到△AE′F′.连接CE′BF′.
①若BF′=6,求CE′的长;
②若∠EBC=∠BAC=36°,在图②的旋转过程中,当CE′∥AB时,直接写出旋转角α的大小.
【答案】(1)答案见解析;(2)①6;②36°或72°.
【解析】试题分析:(1)根据等腰三角形两底角相等∠B=∠C,再根据平行线的性质得出,∠AFE=∠A,∠AEF=∠C,得出∠AFE=∠AEF,进一步得出结论;
(2)求出AE=AF,再根据旋转的性质可得∠E′AC=∠F′AB,AE′=AF′,然后利用“边角边”证明△CAE′和△BAF′全等,根据全等三角形对应边相等证明即可;
(3)把△AEF绕点A逆时针旋转AE′与过点C与AB平行的直线相交于M、N,然后分两种情况,根据等腰梯形的性质和等腰三角形的性质分别求解即可.
试题解析:(1)证明:∵AB=AC,
∴∠ABC=∠C,
∵EF∥BC,
∴∠AFE=∠A,∠AEF=∠C,
∴∠AFE=∠AEF,
∴AE=AF.
(2)①由旋转的性质得,∠E′AC=∠F′AB,AE′=AF′,
在△CAE′和△BAF′中,
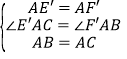 ,
,
∴△CAE′≌△BAF′(SAS),
∴CE′=BF′=6;
②由(1)可知AE=BC,
所以,在△AEF绕点A逆时针旋转过程中,点E经过的路径(圆弧)与过点C且与AB平行的直线l相交于点M、N,如图,
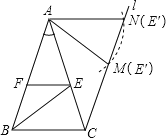
①当点E的像E′与点M重合时,四边形ABCM是等腰梯形,
所以,∠BAM=∠ABC=72°,
又∵∠BAC=36°,
∴α=∠CAM=36°;
②当点E的像E′与点N重合时,
∵CE′∥AB,
∴∠AMN=∠BAM=72°,
∵AM=AN,
∴∠ANM=∠AMN=72°,
∴∠MAN=180°72°×2=36°,
∴α=∠CAN=∠CAM+∠MAN=36°+36°=72°,
综上所述,当旋转角α为36°或72°.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,对角线AC、BD相交于点O,点E、F分别是边AD、AB上的点,连结OE、OF、EF.若AB=7,BC=5![]() ,∠DAB=45°,则①点C到直线AB的距离是_____.②△OEF周长的最小值是________.
,∠DAB=45°,则①点C到直线AB的距离是_____.②△OEF周长的最小值是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A(1,a)是反比例函数![]() 的图象上一点,直线
的图象上一点,直线![]() 与反比例函数
与反比例函数![]() 的图象的交点为点B、D,且B(3,﹣1),求:
的图象的交点为点B、D,且B(3,﹣1),求:
(1)求反比例函数的解析式;
(2)求点D坐标,并直接写出y1>y2时x的取值范围;
(3)动点P(x,0)在x轴的正半轴上运动,当线段PA与线段PB之差达到最大时,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校公布了该校反映各年级学生体育达标情况的两张统计图,该校七、八、九三个年级共有学生800人。甲,乙,丙三个同学看了这两张统计图后,甲说:“七年级的体育达标率最高.”乙说:“八年级共有学生264人。”丙说:“九年级的体育达标率最高。”甲、乙、丙三个同学中,说法正确的是_____________。


查看答案和解析>>
科目:初中数学 来源: 题型:
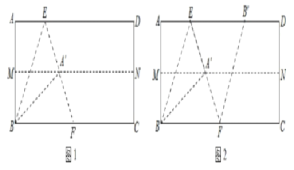
【题目】对一张矩形纸片ABCD进行折叠,具体操作如下:
第一步:先对折,使AD与BC重合,得到折痕MN,展开;
第二步:再一次折叠,使点A落在MN的点A′处,并使折痕经过点B,得到折痕BE,同时,得到线段BA′,EA′,展开,如图1;
第三步:再沿EA′所在的直线折叠,点B落在AD的点B′处,得到折痕EF,同时得到线段B′F,展开,如图2.
(1)证明:∠ABE=30°;
(2)证明:四边形BFB′E为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC与△A'B'C在平面直角坐标系中的位置如图.

(1)分别写出B、B'的坐标:B______;B′______;
(2)若点P(a,b)是△ABC内部一点,则平移后△A'B'C内的对应点P′的坐标为______;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市进行“新城区改造建设”,有甲、乙两种车参加运土,已知5辆甲种车和2辆乙种车一次共可运土64米![]() ,3辆甲种车和1辆乙种车一次共可运土36米
,3辆甲种车和1辆乙种车一次共可运土36米![]() .
.
(1)求甲、乙两种车每辆一次可分别运土多少米![]() ;
;
(2)某公司派甲、乙两种汽车共10辆参加运土,且一次运土总量不低于100米![]() ,求公司最多要派多少辆甲种汽车参加运土.
,求公司最多要派多少辆甲种汽车参加运土.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把6张长为a、宽为b(a>b)的小长方形纸片不重叠地放在长方形ABCD内,未被覆盖的部分(两个长方形)用阴影表示,设这两个长方形的面积的差为S.当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a、b满足( )

A. a=1.5bB. a=2.5bC. a=3bD. a=2b
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com