
分析 (1)根据零指数幂和负整数指数幂运算;
(2)根据积的乘方法则运算;
(3)先利用乘法的交换律得到原式=4×(-$\frac{1}{2}$)×106•10-3,再根据同底数幂的乘法法则运算;
(4)根据零指数幂和负整数指数幂运算.
解答 解:(1)原式=1×$\frac{1}{16}$=$\frac{1}{16}$;
(2)原式=[(-3)×(-$\frac{1}{3}$)]100•(-$\frac{1}{3}$)
=-$\frac{1}{3}$;
(3)原式=4×(-$\frac{1}{2}$)×106•10-3
=-2×103;
(4)原式=1-8+1-3
=-11.
点评 本题考查了整式的混合运算:有乘方、乘除的混合运算中,要按照先乘方后乘除的顺序运算,其运算顺序和有理数的混合运算顺序相似.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
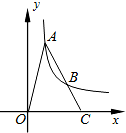 如图,A、B是双曲线y=$\frac{k}{x}$(k>0)上的点,A、B两点的横坐标分别是a、2a,线段AB的延长线交x轴于点C,若S△AOC=6.则k=( )
如图,A、B是双曲线y=$\frac{k}{x}$(k>0)上的点,A、B两点的横坐标分别是a、2a,线段AB的延长线交x轴于点C,若S△AOC=6.则k=( )| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com