
如图,AB是⊙O的直径,AC是弦,直线EF经过点C,AD⊥EF于点D,∠DAC=∠BAC.

(1)求证:EF是⊙O的切线;
(2)求证:AC2=ADAB;
(3)若⊙O的半径为2,∠ACD=30°,求图中阴影部分的面积.
(1)证明见解析;(2)证明见解析;(3) .
.
【解析】
试题分析:(1)连接OC,根据OA=OC推出∠BAC=∠OCA=∠DAC,推出OC∥AD,得出OC⊥EF,根据切线的判定推出即可;
(2)证△ADC∽△ACB,得出比例式,即可推出答案;
(3)求出等边三角形OAC,求出AC、∠AOC,在Rt△ACD中,求出AD、CD,求出梯形OCDA和扇形OCA的面积,相减即可得出答案.
试题解析:(1)证明:连接OC,
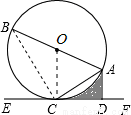
∵OA=OC,
∴∠BAC=∠OCA,
∵∠DAC=∠BAC,
∴∠OCA=∠DAC,
∴OC∥AD,
∵AD⊥EF,
∴OC⊥EF,
∵OC为半径,
∴EF是⊙O的切线.
(2)证明:连接BC,
∵AB为⊙O直径,AD⊥EF,
∴∠BCA=∠ADC=90°,
∵∠DAC=∠BAC,
∴△ACB∽△ADC,
∴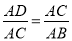 ,
,
∴AC2=ADAB.
(3)【解析】
∵∠ACD=30°,∠OCD=90°,
∴∠OCA=60°,
∵OC=OA,
∴△OAC是等边三角形,
∴AC=OA=OC=2,∠AOC=60°,
∵在Rt△ACD中,AD=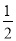 AC=
AC=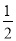 ×2=1,
×2=1,
由勾股定理得:DC=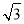 ,
,
∴阴影部分的面积是S=S梯形OCDA-S扇形OCA=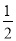 ×(2+1)×
×(2+1)×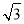 -
-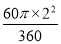 =
= .
.
考点:圆的综合题.


科目:初中数学 来源:2014-2015学年山东省新泰市九年级上学期学业水平模拟数学试卷(解析版) 题型:选择题
一张桌子上摆放着若干个碟子,从三个方向上看在眼里,三种视图如下图所示,则这张桌子上共有碟子为( )

A.6个 B.8个 C.12个 D.17个
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省九年级上学期期末调研数学试卷(解析版) 题型:解答题
(本小题满分8分)如图,矩形ABCD的对角线AC、BD相交于点O,DE∥AC,CE∥BD.
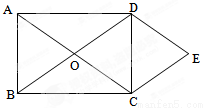
(1)判断四边形OCED的形状,并进行证明;
(2)点E是否在AB的垂直平分线上?若在,请进行证明;若不在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省九年级上学期期末调研数学试卷(解析版) 题型:选择题
某商品计划以每件600元的均价对外销售,后来为加快资金周转,对价格经过两次下调后,决
定以每件486元的均价销售.则平均每次下调的百分率是( ).
A.30% B.20% C.15% D.10%
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省如皋市九年级12月阶段测试数学试卷(解析版) 题型:解答题
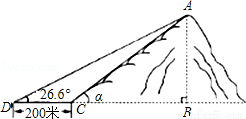
如图,小山岗的斜坡AC的坡度是tanα=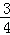 ,在与山脚C距离200米的D处,测得山顶A的仰角为26.6°,求小山岗的高AB(结果取整数:参考数据:sin26.6°=0.45,cos26.6°=0.89,tan26.6°=0.50).
,在与山脚C距离200米的D处,测得山顶A的仰角为26.6°,求小山岗的高AB(结果取整数:参考数据:sin26.6°=0.45,cos26.6°=0.89,tan26.6°=0.50).
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省如皋市九年级12月阶段测试数学试卷(解析版) 题型:填空题
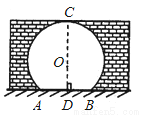
如图是某风景区的一个圆拱形门,路面AB宽为2m,净高CD为5m,则圆拱形门所在圆的半径为 m.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年黑龙江省大庆市林甸县九年级上学期期末检测数学试卷(解析版) 题型:解答题
如图,在正方形ABCD中,点M是BC边上的任一点,连接AM并将线段AM绕M顺时针旋转90°得到线段MN,在CD边上取点P使CP=BM,连接NP,BP.

(1)求证:四边形BMNP是平行四边形;
(2)线段MN与CD交于点Q,连接AQ,若△MCQ∽△AMQ,则BM与MC存在怎样的数量关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省长汀县城区三校九年级12月联考数学试卷(解析版) 题型:解答题
(每小题6分共12分)解方程
(1)2(x+2)2-8=0 ;
(2)2x2-7x+3=0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com