
如图,在正方形ABCD中,点M是BC边上的任一点,连接AM并将线段AM绕M顺时针旋转90°得到线段MN,在CD边上取点P使CP=BM,连接NP,BP.

(1)求证:四边形BMNP是平行四边形;
(2)线段MN与CD交于点Q,连接AQ,若△MCQ∽△AMQ,则BM与MC存在怎样的数量关系?请说明理由.
(1)证明见解析;(2)相等,理由见解析.
【解析】
试题分析:(1)根据正方形的性质可得AB=BC,∠ABC=∠B,然后利用“边角边”证明△ABM和△BCP全等,根据全等三角形对应边相等可得AM=BP,∠BAM=∠CBP,再求出AM⊥BP,从而得到MN∥BP,然后根据一组对边平行且相等的四边形是平行四边形证明即可;
(2)根据同角的余角相等求出∠BAM=∠CMQ,然后求出△ABM和△MCQ相似,根据相似三角形对应边成比例可得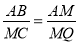 ,再求出△AMQ∽△ABM,根据相似三角形对应边成比例可得
,再求出△AMQ∽△ABM,根据相似三角形对应边成比例可得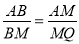 ,从而得到
,从而得到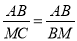 ,即可得解.
,即可得解.
试题解析:(1)证明:在正方形ABCD中,AB=BC,∠ABC=∠B,
在△ABM和△BCP中,
 ,
,
∴△ABM≌△BCP(SAS),
∴AM=BP,∠BAM=∠CBP,
∵∠BAM+∠AMB=90°,
∴∠CBP+∠AMB=90°,
∴AM⊥BP,
∵AM并将线段AM绕M顺时针旋转90°得到线段MN,
∴AM⊥MN,且AM=MN,
∴MN∥BP,
∴四边形BMNP是平行四边形;
(2)【解析】
BM=MC.
理由如下:∵∠BAM+∠AMB=90°,∠AMB+∠CMQ=90°,
∴∠BAM=∠CMQ,
又∵∠ABC=∠C=90°,
∴△ABM∽△MCQ,
∴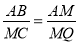
∵△MCQ∽△AMQ,
∴△AMQ∽△ABM,
∴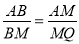
∴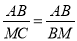
∴BM=MC.
考点:1.相似三角形的判定与性质;2.平行四边形的判定与性质;3.正方形的性质.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源:2014-2015学年山东省滕州市九年级下学期学业水平模拟考试1数学试卷(解析版) 题型:选择题
如图,ΔABC中,AB=AC,BD=CE,BE=CF,若∠A=50°,则∠DEF的度数是
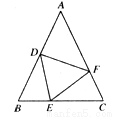
A.75° B.70° C.65° D.60°
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省如皋市九年级12月阶段测试数学试卷(解析版) 题型:解答题
如图,AB是⊙O的直径,AC是弦,直线EF经过点C,AD⊥EF于点D,∠DAC=∠BAC.

(1)求证:EF是⊙O的切线;
(2)求证:AC2=ADAB;
(3)若⊙O的半径为2,∠ACD=30°,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省如皋市九年级12月阶段测试数学试卷(解析版) 题型:选择题
在ΔABC中,BC=10,BC边上的高h=5,点E在AB上,过点E作EF∥BC,交AC于F,D为BC上的一点,连DE、DF.设E到BC的距离为x,则ΔDEF的面积为S关于x的函数图象大致为( )
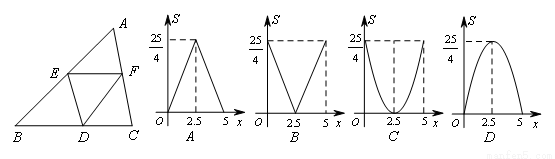
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省如皋市九年级12月阶段测试数学试卷(解析版) 题型:选择题
图中两个转盘分别自由转动一次,当转盘停止转动时,两个指针分别落在某两个数所表示的区域,则这两个数的和是2的倍数或是3的倍数的概率等于( )

A. B.
B.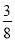 C.
C. D.
D. 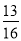
查看答案和解析>>
科目:初中数学 来源:2014-2015学年黑龙江省大庆市林甸县九年级上学期期末检测数学试卷(解析版) 题型:解答题
春秋旅行社为吸引市民组团去天水湾风景区旅游,推出了如图1对话中收费标准.

某单位组织员工去天水湾风景区旅游,共支付给春秋旅行社旅游费用27000元.请问该单位这次共有多少员工去天水湾风景区旅游?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年黑龙江省大庆市林甸县九年级上学期期末检测数学试卷(解析版) 题型:填空题
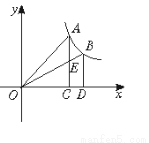
如图,过反比例函数y=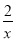 (x>0)图象上任意两点A、B分别作x轴的垂线,垂足分别为C、D,连结OA、OB,设AC与OB的交点为E,△AOE与梯形ECDB的面积分别为S1、S2,比较它们的大小: .
(x>0)图象上任意两点A、B分别作x轴的垂线,垂足分别为C、D,连结OA、OB,设AC与OB的交点为E,△AOE与梯形ECDB的面积分别为S1、S2,比较它们的大小: .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年黑龙江省大庆市林甸县九年级上学期期末检测数学试卷(解析版) 题型:选择题
菱形的两条对角线长分别是6和8,则此菱形的边长是 ( )
A.10 B.8 C.6 D.5
查看答案和解析>>
科目:初中数学 来源:2014-2015学年陕西省七年级上期末测试数学试卷(解析版) 题型:填空题
甲队有32人,乙队有28人,现从乙队抽调x人到甲队,使甲队人数是乙队人数的2倍,依题意可列方程为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com