
【题目】点E在正方形ABCD外,BE=4,CE=2,∠BEC=135°,将△BEC绕点B逆时针旋转得到△BFA,求FE,FC的长. 
【答案】解:由旋转的性质可得:△ABF≌△CBE,
所以∠ABF=∠CBE,BE=BF,
因为正方形ABCD
所以∠ABC=∠ABF+∠CBF=90°,
所以∠EBF=∠CBE+∠CBF=90°,
所以△BEF为等腰Rt△BEF
根据勾股定理:EF=4 ![]() ,
,
因为∠BEC=135°,∠BEF=45°,
所以∠CEF=90°.
所以△BEF为等腰Rt△BEF
根据勾股定理:CF=6
【解析】先由旋转的性质,得出△ABF≌△CBE进而得出BE=BF,再由正方形的得出∠EBF=∠CBE+∠CBF=90°,判断出△BEF为等腰Rt△BEF,再判断出△BEF为等腰Rt△BEF,用勾股定理即可得出结论.
【考点精析】本题主要考查了正方形的性质和旋转的性质的相关知识点,需要掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形;①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了才能正确解答此题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC 中,AB=AC,以AB为直径作⊙O,与BC交于点D,过D作AC的垂线,垂足为E.证明: 
(1)BD=DC;
(2)DE是⊙O切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
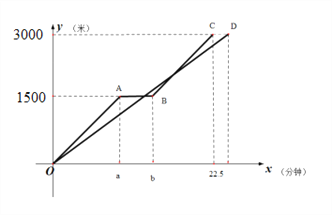
【题目】小军和爸爸同时从家骑自行车去图书馆,爸爸先以150米/分的速度骑行一段时间,休息了5分钟,再以m米/分的速度到达图书馆,小军始终以同一速度骑行,两人行驶的路程y(米)与时间x(分)的关系如图所示,请结合图像,解答下列问题:
(1)a= b= ,m=
(2)若小军的速度是120米/分,求小军在途中与爸爸第二次相遇时,距图书馆的距离;
(3)在(2)的条件下,爸爸自第二次出发至到达图书馆前,何时与小军相距100米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学做一道数学题,已知两个多项式A、B,B=3x2y-5xy+x+7,试求A+B,这位同学把A+B看成A-B,结果求出的答案为6x2y+12xy-2x-9.
(1)请你替这位同学求出的正确答案;
(2)当x取任意数值,A-3B的值是一个定值,求y的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一名工人一天可以加工![]() 个
个![]() 零件,或者加工
零件,或者加工![]() 个
个![]() 零件,每一个
零件,每一个![]() 零件和两个
零件和两个![]() 零件可以组装成一套零件,某车间共有
零件可以组装成一套零件,某车间共有![]() 名工人,问应如何安排这些工人,使加工出来的零件刚好可以配套.
名工人,问应如何安排这些工人,使加工出来的零件刚好可以配套.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两地相距900m,甲乙两人同时从A地出发匀速前往B地,甲到达B地时乙距B地300m.甲到达B地后立刻以原速返回A地,返回途中与乙相遇,相遇后乙也立刻以原速向A地返回.甲、乙离A地的距离y1、y2与他们出发的时间t的函数关系如图所示.
(1)a= ; b= ;
(2)写出点C表示的实际意义 及点C的坐标
(3)甲出发多长时间,两人相距175m?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据图1,图2所提供的信息,解答下列问题: 
(1)2007年海南省城镇居民人均可支配收入为元,比2006年增长%;
(2)求2008年海南省城镇居民人均可支配收入(精确到1元),并补全条形统计图;
(3)根据图1指出:2005﹣2008年海南省城镇居民人均可支配收入逐年(填“增加”或“减少”).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点D在AB的延长线上,BD=OB,点C在圆上,∠CAB=30°. 
(1)求证:DC是⊙O的切线.
(2)若BD=1cm,求AC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com