
【题目】如图1,在平面直角坐标系xOy中,半径为1的⊙O与x轴正半轴和y轴正半轴分别交于A,B两点,直线l:y=kx+2(k<0)与x轴和y轴分别交于P,M两点.
(1)当直线与⊙O相切时,求出点M的坐标和点P的坐标;
(2)如图2,当点P在线段OA上时,直线1与⊙O交于E,F两点(点E在点F的上方)过点F作FC∥x轴,与⊙O交于另一点C,连结EC交y轴于点D.
①如图3,若点P与点A重合时,求OD的长并写出解答过程;
②如图2,若点P与点A不重合时,OD的长是否发生变化,若不发生变化,请求出OD的长并写出解答过程;若发生变化,请说明理由.
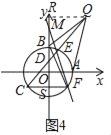
(3)如图4,在(2)的基础上,连结BF,将线段BF绕点B逆时针旋转90°到BQ,若点Q在CE的延长线时,请用等式直接表示线段FC,FQ之间的数量关系.

【答案】(1)![]() ;(2)①
;(2)①![]() ②OD的长度不变;(3)3FQ2=4FC2+2FC
②OD的长度不变;(3)3FQ2=4FC2+2FC
【解析】
(1)先根据题意求出A、B、M、P坐标(P坐标用k表示),由直线与⊙O相切,先设切点为N,则有ON⊥MP且ON=1,因此∠MON可求,故利用三角函数可求OP的长,即求出P的坐标.
(2)①当P与A重合时,k值可求即直线l解析式确定,点F也与P、A重合,C在x轴上为(﹣1,0).因为点E在直线l上且在⊙O上,可求出E坐标,故直线CE解析式可求,即求出CE与y轴交点D.
②要求OD的长即求D的坐标,解题思路与①相同,但由于P与A不重合,直线l和点E、F坐标不确定,可先设E、F坐标,利用直线l与点在⊙O的关系列得方程,得到点E、F横坐标之间的关系.用E、F横坐标表示的点C、E坐标代入求CE解析式,化简后即求出其与y轴交点纵坐标的值.
(3)在(2)的基础上有![]() 可直接使用.由旋转90°联想到构造三垂直全等模型,作QR垂直y轴,即能用F的坐标表示QR、BR等线段长度.又由FC∥QR得相似,对应边的比相等得到用F坐标表示的等式.利用F在⊙O上化简式子,并代入求FQ2,即能得到FQ2与FC的长度关系.
可直接使用.由旋转90°联想到构造三垂直全等模型,作QR垂直y轴,即能用F的坐标表示QR、BR等线段长度.又由FC∥QR得相似,对应边的比相等得到用F坐标表示的等式.利用F在⊙O上化简式子,并代入求FQ2,即能得到FQ2与FC的长度关系.
解:(1)∵半径为1的⊙O与x轴正半轴和y轴正半轴分别交于A,B两点
∴A(1,0),B(0,1),OA=OB=1
直线l:y=kx+2(k<0)中,当x=0时,y=2
∴点M坐标为(0,2),OM=2
当kx+2=0时,解得:![]()
∴点P坐标为![]()
![]()
设直线l与与⊙O相切于点N,
∴ON⊥MP,ON=1
∴∠ONM=∠ONP=90°
∴Rt△OMN中,sin∠OMN=![]()
∴∠OMN=30°
∴Rt△MOP中,tan∠OMP=![]()
∴![]() 解得:
解得:![]() ,
,
∴![]()
∴点P坐标为![]()
(2)①∵P与A重合,FC∥x轴
∴P(1,0),![]() =1,点F与P、A重合
=1,点F与P、A重合
∴k=﹣2,C(﹣1,0)
∴直线l:y=﹣2x+2
∵点E在直线l上,且在⊙O上
∴设E(e,﹣2e+2),则有e2+(﹣2e+2)2=1
解得:e1=1(即为点A,舍去),![]() ,
,
∴![]()
∴点E坐标为![]()
设直线CE解析式为:y=ax+b
∴ 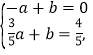 解得:
解得:![]()
∴直线CE与y轴交点![]()
∴![]()
②OD的长度不变.
设点(x,y)在⊙O上,则有x2+y2=1
∴求直线l:y=kx+2与⊙O的交点E、F,即求两方程的公共解
![]()
整理得:(1+k2)x2+4kx+3=0
设E(e,ke+2),F(t,kt+2)
∴![]() ①,et
①,et![]() ②
②
∵FC∥x轴且C在⊙O上
∴C、F关于y轴对称,即C(﹣t,kt+2)
设直线CE解析式为:y=ax+b
∴![]()
③×e得:﹣aet+be=ket+2e⑤
④×t得:aet+bt=ket+2t⑥
⑤+⑥得:(e+t)b=2ket+2(e+t)
∴![]()
把①②式代入得:![]()
∴![]() 即
即![]() 长度不变.
长度不变.
(3)过点Q作QR⊥y轴于R,设CF与y轴交点为S
∴∠BRQ=∠FSB=90°
∵线段BF绕点B逆时针旋转90°到BQ
∴∠FBQ=90°,BQ=BF,即△BFQ是等腰直角三角形
∴∠RBQ+∠SBF=∠RBQ+∠RQB=90°
∴∠RQB=∠SBF
在△RQB与△SBF

∴△RQB≌△SBF(AAS)
∴RQ=SB,BR=SF
设F(t,s),C(﹣t,s)
则FC=2t,RQ=SB=1﹣s,BR=SF=t
∵在(2)的基础上有![]()
∴![]()
∵CS∥RQ,C、D、Q在同一直线上
∴△CDS∽△QDR
∴![]()
∴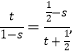
整理得:2s2﹣2t2﹣3s﹣t+1=0
∵点F(t,s)在⊙O上,满足s2+t2=1,
代入整理得:![]()
∵FQ2=BF2+BQ2=2BQ2=2(BR2+RQ2)=2[t2+(1﹣s)2]=4﹣4s=![]()
FC=2t,FC2=4t2
∴3FQ2=4FC2+2FC


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:
【题目】某商店经销一种健身球,已知这种健身球的成本价为每个20元,市场调查发现,该种健身球每天的销售量y(个)与销售单价x(元)有如下关系:y=﹣20x+80(20≤x≤40),设这种健身球每天的销售利润为w元.
(1)求w与x之间的函数关系式;
(2)该种健身球销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种健身球的销售单价不高于28元,该商店销售这种健身球每天要获得150元的销售利润,销售单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
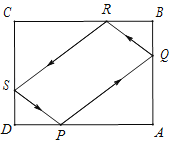
【题目】如图ABCD是一个矩形桌子,一小球从P撞击到Q,反射到R,又从R反射到S,从S反射回原处P,入射角与反射角相等(例如∠PQA=∠RQB等),已知AB=9,BC=12,BR=4.则小球所走的路径的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
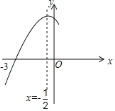
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,其对称轴为直线
,其对称轴为直线![]() ,结合图象分析下列结论:①
,结合图象分析下列结论:①![]() ;②
;②![]() ;③当
;③当![]() 时,
时,![]() 随
随![]() 的增大而增大;④一元二次方程
的增大而增大;④一元二次方程![]() 的两根分别为
的两根分别为![]() ,
,![]() ;⑤
;⑤![]() ;⑥若
;⑥若![]() ,
,![]() 为方程
为方程![]() 的两个根,则
的两个根,则![]() 且
且![]() ,其中正确的结论有( )
,其中正确的结论有( )
A. ![]() 个B.
个B. ![]() 个C.
个C. ![]() 个D.
个D. ![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
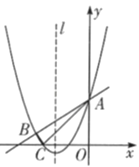
【题目】如图,抛物线y=![]() x2+bx+c与直线y=
x2+bx+c与直线y=![]() x+3分别相交于A,B两点,且此抛物线与x轴的一个交点为C,连接AC,BC.已知A(0,3),C(﹣3,0).
x+3分别相交于A,B两点,且此抛物线与x轴的一个交点为C,连接AC,BC.已知A(0,3),C(﹣3,0).
(1)求抛物线的解析式;
(2)在抛物线对称轴l上找一点M,使|MB﹣MC|的值最大,并求出这个最大值;
(3)点P为y轴右侧抛物线上一动点,连接PA,过点P作PQ⊥PA交y轴于点Q,问:是否存在点P使得以A,P,Q为顶点的三角形与△ABC相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AC=4,BC=2,点D在射线AB上,在构成的图形中,△ACD为等腰三角形,且存在两个互为相似的三角形,则CD的长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
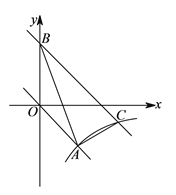
【题目】如图,在平面直角坐标![]() 中,正比例函数
中,正比例函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象经过点
的图象经过点![]() .
.
(![]() )分别求这两个函数的表达式.
)分别求这两个函数的表达式.
(![]() )将直线
)将直线![]() 向上平移
向上平移![]() 个单位长度后与
个单位长度后与![]() 轴交于点
轴交于点![]() ,与反比例函数图象在第四象限内的交点为
,与反比例函数图象在第四象限内的交点为![]() ,连接
,连接![]() 、
、![]() ,求点
,求点![]() 的坐标及
的坐标及![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中装有仅颜色不同的20个小球,其中红球6个,黑球14个
(1)先从袋子中取出x(x>3)个红球后,再从袋子中随机摸出1个球,将“摸出黑球”,记为事件A.请完成下列表格.
事件A | 必然事件 | 随机事件 |
x的值 |
(2)先从袋子中取出m个红球,再放入2m个一样的黑球并摇匀,随机摸出1个球是黑球的概率是![]() ,求m的值.
,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com