
【题目】如图:平行四边形ABCD中,E为AB中点,AF=![]() FD,连E、F交AC于G,则AG:GC=_____.
FD,连E、F交AC于G,则AG:GC=_____.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】定义:如果一个三位数,它的各个数位上的数字都不为零,且满足百位上的数字与个位上的数字的平均数等于十位上的数字,则称这个三位数为开合数.设![]() 为一个开合数,将
为一个开合数,将![]() 的百位数字与个位数字交换位置后得到的新数再与
的百位数字与个位数字交换位置后得到的新数再与![]() 相加的和记为
相加的和记为![]() .例如:852是“开合数”,则
.例如:852是“开合数”,则![]() .
.
(1)已知开合数![]() (
(![]() ,且为
,且为![]() 整数),求
整数),求![]() 的值;
的值;
(2)三位数![]() 是一个开合数,若百位数字小于个位数字,
是一个开合数,若百位数字小于个位数字,![]() 是一个整数,且
是一个整数,且![]() 能被个位数字与百位数字的差整除,请求满足条件的所有
能被个位数字与百位数字的差整除,请求满足条件的所有![]() 值.
值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班为参加学校的大课间活动比赛,准备购进一批跳绳,已知2根![]() 型跳绳和1根
型跳绳和1根![]() 型跳绳共需56元,1根
型跳绳共需56元,1根![]() 型跳绳和2根
型跳绳和2根![]() 型跳绳共需82元.
型跳绳共需82元.
(1)求一根![]() 型跳绳和一根
型跳绳和一根![]() 型跳绳的售价各是多少元?
型跳绳的售价各是多少元?
(2)学校准备购进这两种型号的跳绳共50根,并且![]() 型跳绳的数量不多于
型跳绳的数量不多于![]() 型跳绳数量的3倍,请设计出最省钱的购买方案,并说明理由.
型跳绳数量的3倍,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系xOy中,半径为1的⊙O与x轴正半轴和y轴正半轴分别交于A,B两点,直线l:y=kx+2(k<0)与x轴和y轴分别交于P,M两点.
(1)当直线与⊙O相切时,求出点M的坐标和点P的坐标;
(2)如图2,当点P在线段OA上时,直线1与⊙O交于E,F两点(点E在点F的上方)过点F作FC∥x轴,与⊙O交于另一点C,连结EC交y轴于点D.
①如图3,若点P与点A重合时,求OD的长并写出解答过程;
②如图2,若点P与点A不重合时,OD的长是否发生变化,若不发生变化,请求出OD的长并写出解答过程;若发生变化,请说明理由.
(3)如图4,在(2)的基础上,连结BF,将线段BF绕点B逆时针旋转90°到BQ,若点Q在CE的延长线时,请用等式直接表示线段FC,FQ之间的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校植物园沿路护栏的纹饰部分设计成若干个全等菱形图案,每增加一个菱形图案,纹饰长度就增加dcm,如图所示,已知每个菱形图案的边长为10![]() cm,其中一个内角为60°.
cm,其中一个内角为60°.
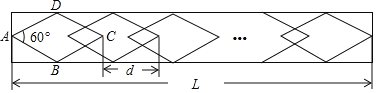
(1)求一个菱形图案水平方向的对角线长;
(2)若d=26,纹饰的长度L能否是6010cm?若能,求出菱形个数;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①所示,已知正方形ABCD和正方形AEFG,连接DG,BE.
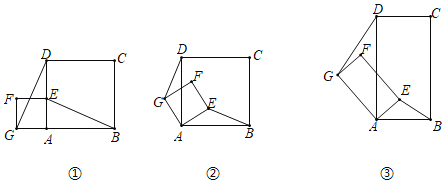
(1)发现:当正方形AEFG绕点A旋转,如图②所示.
①线段DG与BE之间的数量关系是 ;
②直线DG与直线BE之间的位置关系是 ;
(2)探究:如图③所示,若四边形ABCD与四边形AEFG都为矩形,且AD=2AB,AG=2AE时,上述结论是否成立,并说明理由.
(3)应用:在(2)的情况下,连接BG、DE,若AE=1,AB=2,求BG2+DE2的值(直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将两块直角三角板如图1放置,等腰直角三角板![]() 的直角顶点是点
的直角顶点是点![]() ,
,![]() ,直角板
,直角板![]() 的直角顶点
的直角顶点![]() 在
在![]() 上,且
上,且![]() ,
,![]() .三角板
.三角板![]() 固定不动,将三角板
固定不动,将三角板![]() 绕点
绕点![]() 逆时针旋转,旋转角为
逆时针旋转,旋转角为![]()
![]() .
.
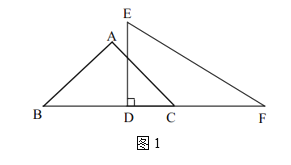
(1)当![]() _______时,
_______时,![]() ;
;
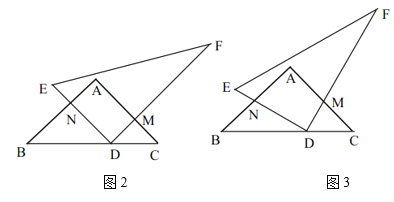
(2)当![]() 时,三角板
时,三角板![]() 绕点
绕点![]() 逆时针旋转至如图2位置,设
逆时针旋转至如图2位置,设![]() 与
与![]() 交于点
交于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,求四边形
,求四边形![]() 的面积.
的面积.
(3)如图3,设![]() ,四边形
,四边形![]() 的面积为
的面积为![]() ,求
,求![]() 关于
关于![]() 的表达式(不用写
的表达式(不用写![]() 的取值范围).
的取值范围).
查看答案和解析>>
科目:初中数学 来源: 题型:
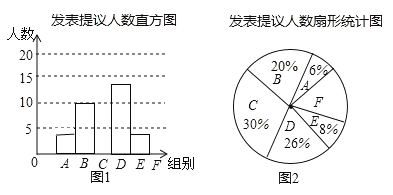
【题目】两会期间,记者随机抽取参会的部分代表,对他们某天发言的次数进行了统计,其结果如表,并绘制了如图所示的两幅不完整的统计图,请结合图中相关数据回答下列问题:
发言次数n | |
A | 0≤n<3 |
B | 3≤n<6 |
C | 6≤n<9 |
D | 9≤n<12 |
E | 12≤n<15 |
F | 15≤n<18 |
(1)求得样本容量为 ,并补全直方图;
(2)如果会议期间组织1700名代表参会,请估计在这一天里发言次数不少于12次的人数;
(3)已知A组发表提议的代表中恰有1为女士,E组发表提议的代表中只有2位男士,现从A组与E组中分别抽一位代表写报告,请用列表法或画树状图的方法,求所抽的两位代表恰好都是男士的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com