
分析 通过观察,得出规律:这类勾股数分别为2n+1,2n(n+1),2n(n+1)+1,由此可写出第7组勾股数及第n组勾股数.
解答 解:∵第一组:3=2×1+1,4=2×1×(1+1),5=2×1×(1+1)+1,
第二组:5=2×2+1,12=2×2×(2+1),13=2×2×(2+1)+1,
第三组:7=2×3+1,24=2×3×(3+1),25=2×3×(3+1)+1,
第四组:9=2×4+1,40=2×4×(4+1)41=2×4×(4+1)+1,
∴第七组勾股数是a=2×7+1=15,b=2×7×(7+1)=112,c=2×7×(7+1)+1=113,即15,112,113;
第n组勾股数是2n+1,2n(n+1),2n(n+1)+1.
点评 此题考查的是勾股数,属于规律性题目,关键是通过观察找出规律求解.


科目:初中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

| 图形 | ① | ② | ③ |
| 正方形的个数 | 8 | 13 | 18 |
| 图形的周长 | 18 | 28 | 38 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 一个三角形中至少有一个角不少于60° | |
| B. | 三角形的中线不可能在三角形的外部 | |
| C. | 周长相等的两个三角形全等 | |
| D. | 三角形的中线把三角形的面积平均分成相等的两部分 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
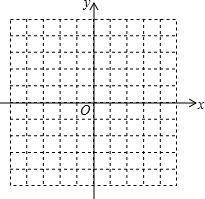 已知在等腰△ABC中,AB=AC,对称轴为x轴,点A的坐标为(-3,0),点B的坐标为(1,3).
已知在等腰△ABC中,AB=AC,对称轴为x轴,点A的坐标为(-3,0),点B的坐标为(1,3).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com