
����Ŀ����ͼ���ھ���![]() �У�
��![]() ��
��![]() ��
��![]() Ϊ�Խ���
Ϊ�Խ���![]() ��һ�㣬��
��һ�㣬��![]() ����
����![]() ��
��![]() ���ֱ�
���ֱ�![]() ��
��![]() ��
��![]() ��
��![]() ������
������![]() �ӵ�
�ӵ�![]() ��������ÿ��1����λ�����ٶ�������
��������ÿ��1����λ�����ٶ�������![]() ���˶�������
���˶�������![]() �ӵ�
�ӵ�![]() ��������ÿ��1����λ�����ٶ����߶�
��������ÿ��1����λ�����ٶ����߶�![]() ����
����![]()
![]()
![]() �����˶�����
�����˶�����![]() Ϊ�����ȱ�
Ϊ�����ȱ�![]() ����֪
����֪![]() ��
��![]() ����ͬʱ����������
����ͬʱ����������![]() ���ص�
���ص�![]() ʱ����ͬʱֹͣ�˶����˶�ʱ��Ϊ
ʱ����ͬʱֹͣ�˶����˶�ʱ��Ϊ![]() ��.
��.
��1�����߶�![]() ������
������![]() �����߶�
�����߶�![]() ��ʱ
��ʱ![]() ���ڶ�����
���ڶ�����
��2�����˶�������![]() �����
�����![]() ���ص��������Ϊ
���ص��������Ϊ![]() ����ֱ��д��
����ֱ��д��![]() ��
��![]() �ĺ�����ϵʽ���Ա���
�ĺ�����ϵʽ���Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3�����ı���![]() �Ƶ�
�Ƶ�![]() ��תһ�ܣ��ڴ˹����У���ֱ��
��תһ�ܣ��ڴ˹����У���ֱ��![]() �ֱ���ֱ��
�ֱ���ֱ��![]() ��
��![]() ���ڵ�
���ڵ�![]() ��
��![]() ����
����![]() ����
����![]() Ϊ�ǵĵ���������ʱ����
Ϊ�ǵĵ���������ʱ����![]() �ij�.
�ij�.
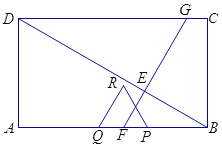
���𰸡���1���߶�BF=4������![]() �����߶�
�����߶�![]() ��ʱt=3����2������������3��
��ʱt=3����2������������3��![]() ��
��![]() ��
��![]() ��
��![]() .
.
��������
��1�����ݾ��ε����ʣ������֪����ͨ����ֱ�������μ�����⣻
��2����Ϊ�������������ͼ�Σ�������������ε����������ͼ�μ��ɵó�����
��3���ȸ��ݽ�ֱ��������,���BF�ij�,�ٸ�����ת���![]() �ij�,�������ı���BCGF��ת������ֲ�ͬλ�ý�������,���DN�ij�.
�ij�,�������ı���BCGF��ת������ֲ�ͬλ�ý�������,���DN�ij�.
��1���߾���ABCD�У�AB=9��AD=![]() ,
,![]()
����ABD=30��BD=![]() ��
��
��DE=2BE��FG��BD��
��DE=4![]() ��BE=2
��BE=2![]()
��![]() ��
��
�൱��R�����߶�CDʱ����PQR�ĸ�Ϊ![]() �����Ϊ6������t=3.
�����Ϊ6������t=3.
��2�����������ͼ��ʾͼ1��ͼ2,ͼ3��ͼ4
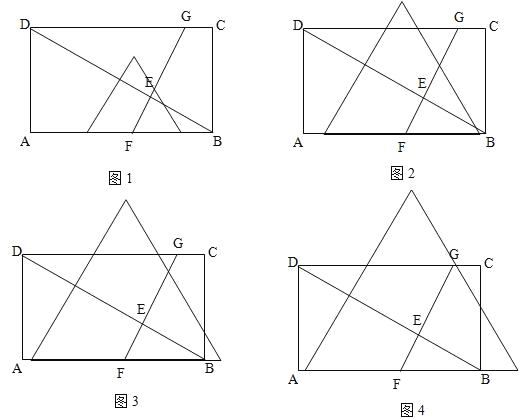
ͼ1��ʾ����![]() ʱ��
ʱ��![]() ��
��
ͼ2��ʾ����![]() ʱ��
ʱ��![]() ��
��
ͼ3 ��ʾ����![]() ʱ��
ʱ��![]()
ͼ4��ʾ����![]() ʱ��
ʱ��![]() ��
��
��3���ɣ�1����BF=4������ת�ɵ�BF'=BF=4����F'BC'=��FBC=90�㣬��BFG=��BF'G'=60�㣬����ͼ5������DMN���ԡ�MDN����MNDΪ�ǵĵ���������ʱ����N=30�㣬
��tan��BNF'=![]() ��
��
��![]() ����BN=4
����BN=4![]() ��
��
��DN=BD+BN=6![]() +4
+4![]() =10
=10![]() ��
��
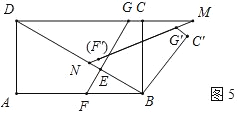
����ͼ6������DMN���ԡ�MDN����NMDΪ�ǵĵ���������ʱ����BNM=60��=��BF'M����ʱ��F'��N�غϣ���BF'=BN=4��
��DN=BD��BN=6![]() ��4��
��4��
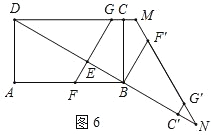
�ʴ�Ϊ��10![]() ��6
��6![]() ��4
��4



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
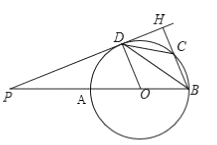
����Ŀ����ͼ���ڡ�O�У���PΪֱ��BA�ӳ�����һ�㣬PD�С�O�ڵ�D������B��BH��PH����HΪ���㣬BH����O�ڵ�C������BD��CD��
��1����֤��BDƽ�֡�ABH��
��2����CD=2����ABD=30�������O��ֱ���ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ��ʵ���ù�����飬�ڹ������ʻ5���Ӻ��뿪�����ǰ2�������ٶ�v����/�֣���ʱ��t���֣�������κ���v=at2�������������ٶ�v����/�֣���ʱ��t���֣����㷴����������ϵ����ͼ������ԱߵIJ����Dz�õ���1����ĩ���ٶ�Ϊ2��/�֣���
��1�����κ����ͷ����������Ĺ�ϵʽ��
��2�������ڹ������ʻ������ٶȣ�

���𰸡���1��v=![]() ��2��t��5�� ��2��8��/��
��2��t��5�� ��2��8��/��
����������������1����ͼ���֪ǰһ���ӹ��㣨1��2������������ʱ���㣨2��8�����ֱ����ô���ϵ��������ú�������ʽ��
��2����t=2���루1���ж��κ�������ʽ���ɣ�
��⣺��1��v=at2��ͼ���㣨1��2����
��a=2��
����κ����Ľ���ʽΪ��v=2t2����0��t��2����
�跴���������Ľ���ʽΪv=![]() ��
��
������֪��ͼ���㣨2��8����
��k=16��
�෴���������Ľ���ʽΪv=![]() ��2��t��5����
��2��t��5����
��2���߶��κ���v=2t2����0��t��2����ͼ�����ϣ��Գ���Ϊy�ᣬ
�൯���ڹ������ʻ������ٶ���2��ĩ��Ϊ8��/�֣�
�㾦�����⿼���˷����������Ͷ��κ�����Ӧ�ã�����Ĺؼ��Ǵ�ͼ�еõ��ؼ��Ե���Ϣ���Ա�����ȡֵ��Χ��ͼ���������ĵ�����꣮
�����͡������
��������
24
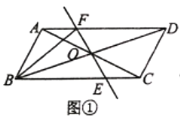
����Ŀ���Ķ����ϣ�С��ͬѧ��������һ�����ɣ�����������ȵĵ��������Σ�������й����Ķ��ǵĶ��㣬�������ǵĵǶ��������������γ�һ����תȫ�ȵ������Σ�С�ְѾ���������ɵ�ͼ�γ�Ϊ�������֡�ͼ�Σ���ͼ1���ڡ������֡�ͼ���У�С�ַ�������BAC=��DAE��AB=AC��AD=AE����BD=CE��
��1����ͼ1��֤��С�ֵķ��֣�
����С��ͬѧ�ܽ���ɣ����조�����֡�ͼ���������������⣺
��2����ͼ2��AB=BC����ABC=��BDC=60�㣬��֤��AD+CD=BD��
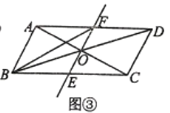
��3����ͼ3������ABC�У�AB=AC����BAC=m�㣬��EΪ��ABC��һ�㣬��DΪBC�е㣬��EBC=��ACF��ED��FD������EAF�Ķ������ú���m��ʽ�ӱ�ʾ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��������һ�����ϣ�ƽ��ÿ����۳�100�䣬ÿ������Ϊ120Ԫ��Ϊ������������������ٿ�棬�������ʵ����ۣ��ݲ��㣬��ÿ�併��2Ԫ����ÿ��ɶ��۳�4�䣮
��1�����Ҫʹÿ�����۸����ϻ���14000Ԫ����ÿ��Ӧ���۶���Ԫ��
��2��ÿ�����۸����ϻ����ܴﵽ14500Ԫ�����ܣ���ÿ��Ӧ���۶��٣������ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
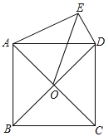
����Ŀ����ͼ��������ABCD�ĶԽ��߽��ڵ�O����ADΪ��������Rt��ADE����AED=90�㣬����OE��DE=6��OE=8![]() ������һֱ�DZ�AE�ij�Ϊ_____��
������һֱ�DZ�AE�ij�Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ֱ�д������1��2��3�����ſ�Ƭ��ע�������ſ�Ƭ����״����С���ʵأ���ɫ������������ȫ��ͬ���������Ϸ��������ϣ������ſ�Ƭ����ȥ���κβ��ϴ�Ⱥ������Ϸ��������ϣ������������ȡһ�ſ�Ƭ���Ǹÿ�Ƭ�ϵ�����Ϊx���ٰ�ʣ�µ����ſ�Ƭϴ�Ⱥ������Ϸ��������ϣ��ٴ������ſ�Ƭ�������ȡһ�ſ�Ƭ���Ǹÿ�Ƭ�ϵ�����Ϊy��
��1�����б�������״ͼ������״ͼҲ������ͼ���е�һ�ַ�����д����x��y�����п��ܳ��ֵĽ����
��2����ȡ�������ſ�Ƭ�ϵ�����֮��Ϊż���ĸ���P��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
�У�![]() ���Խ���
���Խ���![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ����ֱ��
����ֱ��![]() �Ƶ�
�Ƶ�![]() ˳ʱ����תһ���Ƕ�
˳ʱ����תһ���Ƕ�![]() ��
��![]() �����ֱ��߶�
�����ֱ��߶�![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() ����֪
����֪![]() ��
��![]() ������
������![]() .
.

��1����ͼ�٣�����ת�Ĺ����У���д���߶�![]() ��
��![]() ��������ϵ����֤����
��������ϵ����֤����
��2����ͼ�ڣ���![]() ʱ����д���߶�
ʱ����д���߶�![]() ��
��![]() ��������ϵ����֤����
��������ϵ����֤����
��3����ͼ�ۣ���![]() ʱ����
ʱ����![]() �����.
�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
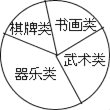
����Ŀ��ijУѧ�������������꼶ѧ���μӡ������ࡱ�����黭�ࡱ���������ࡱ���������ࡱ����У���γ̵�������
��1��ȷ�����鷽ʽʱ����ͬѧ˵�����ҵ����꼶��1����ȥ����ȫ��ͬѧ������ͬѧ˵������ѧʱ�ҵ�У�ſ�������鲿��ͬѧ������ͬѧ˵�����ҵ����꼶ÿ�����������һ��������ͬѧ������ָ����λͬѧ�ĵ��鷽ʽ�������
��� | Ƶ���������� | Ƶ�� |
������ | 0.25 | |
�黭�� | 20 | 0.20 |
������ | 15 | b |
������ | ||
�ϼ� | a | 1.00 |
��2�����Dz�������Ϊ�����ĵ��鷽���ռ����ݣ�����������ͼ��ʾ��ͳ�Ʊ�������ͳ��ͼ��
�����������ͼ���ṩ����Ϣ����������⣺
��a=_____��b=_____��
��������ͳ��ͼ�У�����������Ӧ���ε�Բ�ĽǵĶ�����_____��
������У���꼶��ѧ��560�ˣ�������ƴ�Լ�ж���ѧ���μ�������У���γ̣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com