
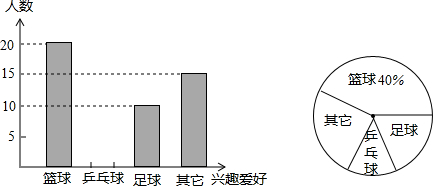
分析 (1)根据篮球的人数和所占的百分比,即可求出总人数;
(2)用总人数减去篮球、足球和其它的人数求出喜欢乒乓球活动的学生数,从而补全统计图;
(3)用该校的总人数乘以喜欢足球活动的人数所占的百分比即可.
解答 解:(1)根据题意得:
$\frac{20}{40%}$=50(名),
答:该校对50名学生进行了抽样调查;
(2)本次抽样调查中最喜欢乒乓球活动的学生数是:50-20-10-15=5(人),
补图如下: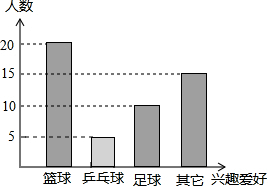
(3)根据题意得:
1800×$\frac{10}{50}$=360(人),
答:全校学生中最喜欢足球活动的人数约为360人.
点评 本题考查的是条形统计图的综合运用.读懂统计图,从统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | [x-(2y+1)]2 | B. | [x+(2y+1)]2 | C. | [x-(2y-1)][x+(2y-1)] | D. | [(x-2y)+1][(x-2y)-1] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com