
【题目】如图,抛物线y=x2﹣bx+c交x轴于点A(1,0),交y轴于点B,对称轴是x=2.

(1)求抛物线的解析式;
(2)点P是抛物线对称轴上的一个动点,是否存在点P,使△PAB的周长最小?若存在,求出点P的坐标;若不存在,请说明理由.
【答案】(1)y=x2﹣4x+3;(2)P的坐标为:(2,1).
【解析】
试题分析:(1)根据抛物线经过点A(1,0),对称轴是x=2列出方程组,解方程组求出b、c的值即可;
(2)因为点A与点C关于x=2对称,根据轴对称的性质,连接BC与x=2交于点P,则点P即为所求,求出直线BC与x=2的交点即可.
解:(1)由题意得, ,
,
解得b=4,c=3,
∴抛物线的解析式为.y=x2﹣4x+3;
(2)∵点A与点C关于x=2对称,
∴连接BC与x=2交于点P,则点P即为所求,
根据抛物线的对称性可知,点C的坐标为(3,0),
y=x2﹣4x+3与y轴的交点为(0,3),
∴设直线BC的解析式为:y=kx+b,
![]() ,
,
解得,k=﹣1,b=3,
∴直线BC的解析式为:y=﹣x+3,
则直线BC与x=2的交点坐标为:(2,1)
∴点P的坐标为:(2,1).



科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=﹣x2+2x+3与x轴交于A,B,与y轴交于C,抛物线的顶点为D,直线l过C交x轴于E(4,0).
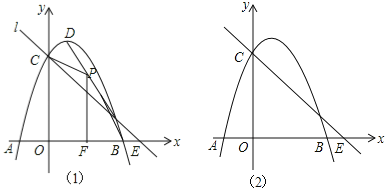
(1)写出D的坐标和直线l的解析式;
(2)P(x,y)是线段BD上的动点(不与B,D重合),PF⊥x轴于F,设四边形OFPC的面积为S,求S与x之间的函数关系式,并求S的最大值;
(3)点Q在x轴的正半轴上运动,过Q作y轴的平行线,交直线l于M,交抛物线于N,连接CN,将△CMN沿CN翻转,M的对应点为M′.在图2中探究:是否存在点Q,使得M′恰好落在y轴上?若存在,请求出Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列等式从左到右的变形是因式分解的是( )
A. x(x﹣2)=x2﹣2xB. x2+2xy+1=x(x+2y)+1
C. 15a2b=3a25bD. a2b2﹣1=(ab+1)(ab﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列条件中,不能判断四边形ABCD是平行四边形的是( )
A.∠A=∠C,∠B=∠D B.AB∥CD,AB=CD
C.AB=CD,AD∥BC D.AB∥CD,AD∥BC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com