在直角坐标系中,已知:A(-1,0),B(3,0),C(0,2),以A、B、C、D为顶点的四边形是平行四边形,则D点的坐标为________.
(2,-2)或(-4,2)或(4,2)
分析:根据题意分情况进行讨论,按照不同的情况画出图形:
(1)以AB为对角线,作DM⊥x轴于点M,DN⊥y轴于点N,即可推出四边形NDMA为矩形,得DN=MO,根据A(-1,0),B(3,0),C(0,2),求出OA=1,OB=3,OC=2,根据平行四边形的性质和平行线的性质求证△COA≌△DMB,即可求出MD的长度,然后根据OB的长度即可求出OM的长度,最后根据D点所在的象限,即可求出D点的坐标;
(2)以AC为对角线时,作DH⊥x轴于点H,首先根据A点、B点、C点的坐标,求出OA=1,OB=3,OC=2,然后根据平行四边形的性质推出CD

AB,通过计算即可求出CD的长度,再根据平行线的性质推出DH=OC=2,最后根据D点在第三象限,即可推出D点的坐标;
(3)以BC为对角线,作DE⊥x轴于点E,首先根据A点、B点、C点的坐标,求出OA=1,OB=3,OC=2,然后根据平行四边形的性质推出CD

AB,通过计算即可求出CD=4,再根据平行线间的距离相等求出DE=OC=2,最后根据D点在第一象限,即可推出D点的坐标为(4,2).
解答:(1)如图1,以AB为对角线时,
作DM⊥x轴于点M,DN⊥y轴于点N,
∵x轴垂直于y轴,
∴四边形NDMA为矩形,
∴DN=MO,
∵A(-1,0),B(3,0),C(0,2),
∴OA=1,OB=3,OC=2,
∵?ACBD,
∴AC

BD,
∴∠DBM=∠CAB,
∵∠COA=∠DMB=90°,
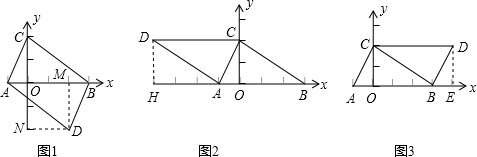
∴在△COA和△DMB中,
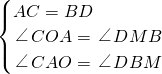
,
∴△COA≌△DMB(AAS),
∴BM=OA=1,MD=OC=2,
∵OB=3,
∴DN=MO=OB-MB=3-1=2,
∵D点在第四象限内,
∴D点的坐标为(2,-2),
(2)如图2,以AC为对角线时,
作DH⊥x轴于点H,
∵A(-1,0),B(3,0),C(0,2),
∴OA=1,OB=3,OC=2,
∵?ABCD,
∴CD

AB,
∴CD=AB=OA+OB=1+3=4,
∵OC⊥HB,
∴DH=OC=2,
∵D点在第三象限,
∴D点的坐标为(-4,2),
(3)如图3,以BC为对角线,
作DE⊥x轴于点E,
∵A(-1,0),B(3,0),C(0,2),
∴OA=1,OB=3,OC=2,
∵?ABDC,
∴CD

AB,
∴CD=AB=OA+OB=1+3=4,
∵OC⊥AE,
∴DE=OC=2,
∵D点在第一象限,
∴D点的坐标为(4,2).
故答案为(2,-2)或(-4,2)或(4,2).
点评:本题主要考查平行四边形的性质,平行线的性质,全等三角形的判定与性质,坐标与图形的性质等知识点,关键在于根据题意分情况进行讨论,正确的画出图形、作辅助线,熟练运用数形结合的思想和相关的性质定理推出全等的三角形、相等的线段.

 AB,通过计算即可求出CD的长度,再根据平行线的性质推出DH=OC=2,最后根据D点在第三象限,即可推出D点的坐标;
AB,通过计算即可求出CD的长度,再根据平行线的性质推出DH=OC=2,最后根据D点在第三象限,即可推出D点的坐标; AB,通过计算即可求出CD=4,再根据平行线间的距离相等求出DE=OC=2,最后根据D点在第一象限,即可推出D点的坐标为(4,2).
AB,通过计算即可求出CD=4,再根据平行线间的距离相等求出DE=OC=2,最后根据D点在第一象限,即可推出D点的坐标为(4,2). BD,
BD,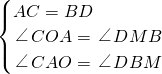 ,
, AB,
AB, AB,
AB,


 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案 如图,在直角坐标系中,已知直线y=kx+6与x轴、y轴分别交于A、B两点,且△ABO的面积为12.
如图,在直角坐标系中,已知直线y=kx+6与x轴、y轴分别交于A、B两点,且△ABO的面积为12.