
【题目】如图,直线y=2x+3与y轴交于A点,与反比例函数y=![]() (x>0)的图象交于点B,过点B作BC⊥x轴于点C,且C点的坐标为(1,0).
(x>0)的图象交于点B,过点B作BC⊥x轴于点C,且C点的坐标为(1,0).

(1)求反比例函数的解析式;
(2)点D(a,1)是反比例函数y=![]() (x>0)图象上的点,在x轴上是否存在点P,使得PB+PD最小?若存在,求出点P的坐标;若不存在,请说明理由.
(x>0)图象上的点,在x轴上是否存在点P,使得PB+PD最小?若存在,求出点P的坐标;若不存在,请说明理由.
【答案】(1)y=![]() ;(2)P(
;(2)P(![]() ,0).
,0).
【解析】
试题分析: (1)把x=1代入y=2x+3中,可求得B点坐标为(1,5),再带到反比例函数解析式中可求得反比例函数解析式;(2)作D关于x轴的对称点D′,连接BD′,与x轴交点即为点P.
试题解析:(1)∵BC⊥x轴于点C,且C点的坐标为(1,0),∴把x=1代入y=2x+3中,y=2+3=5,∴点B的坐标为(1,5),又∵点B(1,5)在反比例函数y=![]() 上,∴k=1×5=5,∴反比例函数的解析式为:y=
上,∴k=1×5=5,∴反比例函数的解析式为:y=![]() ;
;
(2)将点D(a,1)代入y=![]() ,得:a=5,∴点D坐标为(5,1),则点D(5,1)关于x轴的对称点为D′(5,﹣1),设过B(1,5)、D′(5,﹣1)的直线解析式为:y=kx+b,可得
,得:a=5,∴点D坐标为(5,1),则点D(5,1)关于x轴的对称点为D′(5,﹣1),设过B(1,5)、D′(5,﹣1)的直线解析式为:y=kx+b,可得![]() ,解得
,解得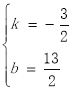 ,
,
∴直线BD′的解析式为:y=﹣![]() x+
x+![]() ,直线BD′与x轴的交点即为所求点P,当y=0时,得:﹣
,直线BD′与x轴的交点即为所求点P,当y=0时,得:﹣![]() x+
x+![]() =0,解得:x=
=0,解得:x=![]() ,故点P的坐标为(
,故点P的坐标为(![]() ,0).
,0).



 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:
【题目】(10分)如图,AB//CD,AE平分MAB交CD于点F,NF⊥CD,垂足为点F,
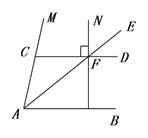
(1)求证:CAF=EFD
(2)若MCD=80,求NFE的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的正方形网格内有一直角坐标系,其中,A点为(-3,0),B点为(-1,2)

(1)C点的坐标为 ;
(2)依次连接ABC得到三角形,将三角形ABC先向右移动3个单位再向下移动2个单位,得到三角形A'B'C',请在图中作出平移后的图形,并写出三个顶点A'、B' 及C' 的坐标;
(3)连接C'C、B'B,直接写出四边形CC' B'B的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
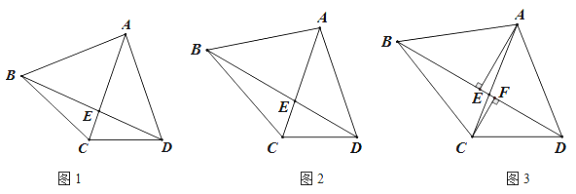
【题目】在四边形ABCD中,AC、BD交于点E,且∠ACD=∠ADC.
(1)如图1,若AB=AD,求证:∠BAC=2∠BDC;
(2)如图2,在(1)的条件下,若∠BDC=30°,求证:BC=AC.
(3)如图3,若BC=AD,∠BDC=30°,过A作AE⊥BD于E,过C作CF⊥BD于F, 且EF:BE=2:11,DF=9,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)阅读:我们知道,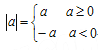 于是要解不等式
于是要解不等式![]() ,我们可以分两种情况去掉绝对值符号,转化为我们熟悉的不等式,按上述思路,我们有以下解法:
,我们可以分两种情况去掉绝对值符号,转化为我们熟悉的不等式,按上述思路,我们有以下解法:
解:(1)当![]() ,即
,即![]() 时:
时: ![]()
解这个不等式,得: ![]()
由条件![]() ,有:
,有:![]()
(2)当![]() < 0,即 x < 3时,
< 0,即 x < 3时,![]()
解这个不等式,得: ![]()
由条件x < 3,有: ![]() < 3
< 3
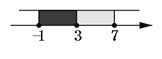
∴ 如图, 综合(1)、(2)原不等式的解为:![]()
根据以上思想,请探究完成下列2个小题:
(1)![]() ; (2)
; (2)![]() 。
。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为加强中小学生安全和禁毒教育,某校组织了“防溺水、交通安全、禁毒”知识竞赛,为奖励在竞赛中表现优异的班级,学校准备从体育用品商场一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),购买1个足球和1个篮球共需159元;足球单价是篮球单价的2倍少9元.
(1)求足球和篮球的单价各是多少元?
(2)根据学校实际情况,需一次性购买足球和篮球共20个,但要求购买足球和篮球的总费用不超过1550元,学校最多可以购买多少个足球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“过关游戏”规定:在过第n关时要将一颗质地均匀的骰子(六个面上分别刻有1到6的点数)抛掷n次,若n次抛掷所出现的点数之和大于n2,则算过关;否则不算过关,则能过第二关的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算与化简:
(1)(﹣5)﹣(+3)﹣(﹣7)+(﹣9)
(2)(﹣3)3÷2![]() ×(﹣
×(﹣![]() )2
)2
(3)(﹣![]() +
+![]() ﹣
﹣![]() )÷(﹣
)÷(﹣![]() )
)
(4)8﹣23÷(﹣4)×|2﹣(﹣3)2|
(5)化简:4(3x2y﹣xy2)﹣6(﹣xy2+3x2y)
(6)化简求值:2(2a2+![]() ab﹣1)﹣2(﹣3a2+ab+1),其中a=﹣4,b=
ab﹣1)﹣2(﹣3a2+ab+1),其中a=﹣4,b=![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com