【题目】数轴上表示整数的点称为整点，某数轴的单位长度是1厘米，若在这个数轴上随意画一条15厘米的线段AB，则AB盖住的整数点的个数共有（ ）个
A. 13或14个 B. 14或15个 C. 15或16个 D. 16或17个
【答案】C
【解析】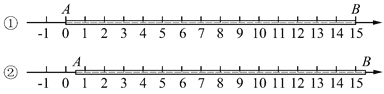
若在数轴上随意画线段AB，其左侧端点A的位置存在两种可能性：一种可能是点A与数轴上某一个整点重合(如图中数轴①所示；为清楚起见，图中用长方形代表线段AB)，另一种可能是点A落在数轴上某两个整点之间的区域内(如图中数轴②所示). 因为线段AB的长是一个定值，所以当线段左侧端点A的位置确定时线段右侧端点B的位置也随之确定.
(1) 分析图中的数轴①可知，由于数轴的单位长度为1厘米，线段AB的长为15厘米，且左侧端点A与一个整点重合，所以线段AB的两个端点各自盖住1个整点，线段的其他部分盖住了14个整点，故线段AB一共盖住了16个整点.
(2) 分析图中的数轴②可知，由于数轴的单位长度为1厘米，线段AB的长为15厘米，且左侧端点A落在两个整点之间的区域内，所以线段AB的两个端点均无法盖住任何整点，线段的其他部分盖住了15个整点，故线段AB一共盖住了15个整点.
综上所述，线段AB盖住的整点的个数共有15或16个.
故本题应选C.
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】△ADE中，AE=AD，∠EAD=90°．
（1）如图（1），若EC、DB分别平分∠AED、∠ADE，交AD、AE于点C、B，连接BC．请你判断AB、AC是否相等，并说明理由；
（2）△ADE的位置保持不变，将（1）中的△ABC绕点A逆时针旋转至图
（2）的位置，CD、BE相交于O，请你判断线段BE与CD的位置关系及数量关系，并说明理由；
（3）在（2）的条件下，若CD=6，试求四边形CEDB的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】 如图，在△ABC中，点D，E分别在边AC，AB上，BD与CE交于点O，给出下列三个条件：①∠EBO=∠DCO；②BE=CD；③OB=OC．
（1）上述三个条件中，由哪两个条件可以判定△ABC是等腰三角形？（用序号写出所有成立的情形）
（2）请选择（1）中的一种情形，写出证明过程．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】从三角形（不是等腰三角形）一个顶点引出一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中有一个为等腰三角形，另一个与原三角形相似，我们把这条线段叫做这个三角形的完美分割线。
（1）如图1，在△ABC中，CD为角平分线，∠A=40°，∠B=60°，求证：CD为△ABC的完美分割线；
（2）在△ABC中，∠A=48°，CD是△ABC的完美分割线，且△ACD为等腰三角形，求∠ACB的度数；
（3）如图2，△ABC中，AC=2，BC=
，CD是△ABC的完美分割线，且△ACD是以CD为底边的等腰三角形，求完美分割线CD的长。
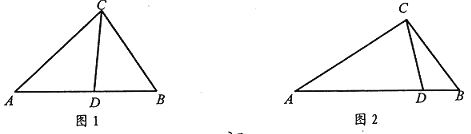
查看答案和解析>>
科目：初中数学 来源： 题型：
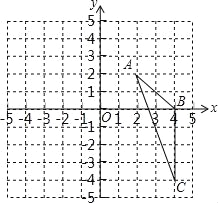
【题目】(2016广西省南宁市第20题)如图，在平面直角坐标系中，已知△ABC三个顶点的坐标分别是A（2，2），B（4，0），C（4，﹣4）
（1）请画出△ABC向左平移6个单位长度后得到的△A1B1C1；
（2）以点O为位似中心，将△ABC缩小为原来的
，得到△A2B2C2，请在y轴右侧画出△A2B2C2，并求出∠A2C2B2的正弦值．
查看答案和解析>>
科目：初中数学 来源： 题型：
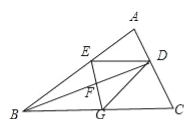
【题目】如图，BD是△ABC的角平分线，它的垂直平分线分别交AB，BD，BC于点E，F，G，连接ED，DG．
（1）请判断四边形EBGD的形状，并说明理由；
（2）若∠ABC=30°，∠C=45°，ED=2
，点H是BD上的一个动点，求HG+HC的最小值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
