
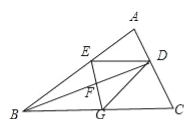
【题目】如图,BD是△ABC的角平分线,它的垂直平分线分别交AB,BD,BC于点E,F,G,连接ED,DG.
(1)请判断四边形EBGD的形状,并说明理由;
(2)若∠ABC=30°,∠C=45°,ED=2![]() ,点H是BD上的一个动点,求HG+HC的最小值.
,点H是BD上的一个动点,求HG+HC的最小值.
【答案】(1)四边形EBGD是菱形,理由见解析;(2)![]() .
.
【解析】
试题分析:(1)四边形EBGD是菱形,根据已知条件易证△EFD≌△GFB,可得ED=BG,所以BE=ED=DG=GB,即可判定四边形EBGD是菱形.(2)作EM⊥BC于M,DN⊥BC于N,连接EC交BD于点H,此时HG+HC最小,在RT△EMC中,求出EM、MC即可解决问题.
试题解析:(1)四边形EBGD是菱形.
理由:∵EG垂直平分BD,
∴EB=ED,GB=GD,
∴∠EBD=∠EDB,
∵∠EBD=∠DBC,
∴∠EDF=∠GBF,
在△EFD和△GFB中,
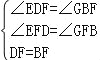 ,
,
∴△EFD≌△GFB,
∴ED=BG,
∴BE=ED=DG=GB,
∴四边形EBGD是菱形.
(2)作EM⊥BC于M,DN⊥BC于N,连接EC交BD于点H,此时HG+HC最小,
在RT△EBM中,∵∠EMB=90°,∠EBM=30°,EB=ED=2![]() ,
,
∴EM=![]() BE=
BE=![]() ,
,
∵DE∥BC,EM⊥BC,DN⊥BC,
∴EM∥DN,EM=DN=![]() ,MN=DE=2
,MN=DE=2![]() ,
,
在RT△DNC中,∵∠DNC=90°,∠DCN=45°,
∴∠NDC=∠NCD=45°,
∴DN=NC=![]() ,
,
∴MC=3![]() ,
,
在RT△EMC中,∵∠EMC=90°,EM=![]() .MC=3
.MC=3![]() ,
,
∴EC=![]() =
=![]() =10.
=10.
∵HG+HC=EH+HC=EC,
∴HG+HC的最小值为10.


科目:初中数学 来源: 题型:
【题目】数轴上表示整数的点称为整点,某数轴的单位长度是1厘米,若在这个数轴上随意画一条15厘米的线段AB,则AB盖住的整数点的个数共有( )个
A. 13或14个 B. 14或15个 C. 15或16个 D. 16或17个
查看答案和解析>>
科目:初中数学 来源: 题型:
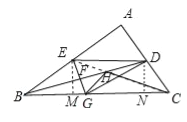
【题目】(1)发现
如图1,点A为线段BC外一动点,且BC=![]() ,AB=
,AB=![]() .
.
填空:当点A位于__________________时,线段AC的长取得最大值,且最大值为_____________.
(用含![]() ,
,![]() 的式子表示)
的式子表示)
(2)应用
点A为线段BC外一动点,且BC=3,AB=1.如图2所示,分别以AB,AC为边,作等边三角形ABD和等边三角形ACE,连接CD,BE.
①请找出图中与BE相等的线段,并说明理由;
②直接写出线段BE长的最大值.

(3)拓展
如图3,在平面直角坐标系中,点A的坐标为(2 , 0),点B的坐标为(5 , 0),点P为线段AB外一动点,且PA=2,PM=PB,∠BPM=90°.请直接写出线段AM长的最大值及此时点P的坐标.
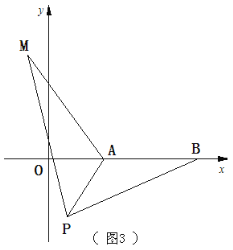
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式从左到右的变形为分解因式的是( )
A.m2-m-6=(m+2)(m-3)
B.(m+2)(m-3)=m2-m-6
C.x2+8x-9=(x+3)(x-3)+8x
D.18x3y2=3x3y2·6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列关于角的说法正确的是( )
A. 两条射线组成的图形叫做角 B. 角的大小与这个角的两边的长短无关
C. 延长一个角的两边 D. 角的两边是射线,所以角不可度量
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com