
【题目】如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A( ![]() ,0),B(0,4),则点B2014的横坐标为 .
,0),B(0,4),则点B2014的横坐标为 . 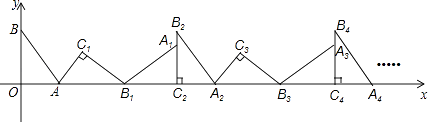
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的中线,∠ADC=45°,把△ABC沿着直线AD对折,点C落在点E的位置,如果BC=12,那么线段BE的长度为( ) 
A.12
B.12 ![]()
C.6 ![]()
D.4 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC是等腰直角三角形,∠BAC=90°,AB=AC四边形ADEF是正方形,点B、C分别在边AD、AF上,此时BD=CF,BD⊥CF成立. 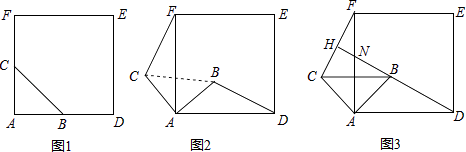
(1)当△ABC绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明,若不成立,请说明理由;
(2)当△ABC绕点A逆时针旋转45°时,如图3,延长BD交CF于点H.求证:BD⊥CF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=x2+(k﹣1)x﹣k与直线y=kx+1交于A,B两点,点A在点B的左侧.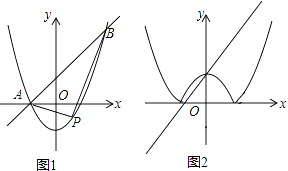
(1)如图1,当k=1时,直接写出A,B两点的坐标;
(2)在(1)的条件下,点P为抛物线上的一个动点,且在直线AB下方,试求出△ABP面积的最大值及此时点P的坐标;
(3)如图2,抛物线y=x2+(k﹣1)x﹣k(k>0)与x轴交于点C、D两点(点C在点D的左侧),抛物线在x轴下方的部分沿x轴翻折得到与原抛物线剩余的部分组成如图所示的图形,若直线y=kx+1与这个图形只有两个公共点,请求出此时k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学兴趣小组研究某型号冷柜温度的变化情况,发现该冷柜的工作过程是:当温度达到设定温度﹣20℃时,制冷停止,此后冷柜中的温度开始逐渐上升,当上升到﹣4℃时,制冷开始,温度开始逐渐下降,当冷柜自动制冷至﹣20℃时,制冷再次停止,…,按照以上方式循环进行. 同学们记录了44min内15个时间点冷柜中的温度y(℃)随时间x(min)的变化情况,制成下表:
时间x/min | … | 4 | 8 | 10 | 16 | 20 | 21 | 22 | 23 | 24 | 28 | 30 | 36 | 40 | 42 | 44 | … |
温度y/℃ | … | ﹣20 | ﹣10 | ﹣8 | ﹣5 | ﹣4 | ﹣8 | ﹣12 | ﹣16 | ﹣20 | ﹣10 | ﹣8 | ﹣5 | ﹣4 | a | ﹣20 | … |
(1)通过分析发现,冷柜中的温度y是时间x的函数. ①当4≤x<20时,写出一个符合表中数据的函数解析式;
②当20≤x<24时,写出一个符合表中数据的函数解析式;
(2)a的值为;
(3)如图,在直角坐标系中,已描出了上表中部分数据对应的点,请描出剩余数据对应的点,并画出当4≤x≤44时温度y随时间x变化的函数图象. 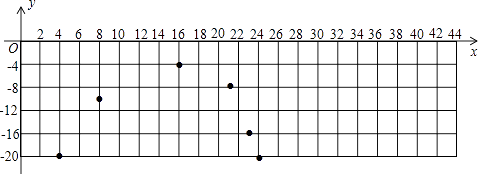
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,过点(﹣2,3)的直线l经过一、二、三象限,若点(0,a),(﹣1,b),(c,﹣1)都在直线l上,则下列判断正确的是( )
A.a<b
B.a<3
C.b<3
D.c<﹣2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com