
����Ŀ����ƽ��ֱ������ϵ�У�������y=x2+��k��1��x��k��ֱ��y=kx+1����A��B���㣬��A�ڵ�B����࣮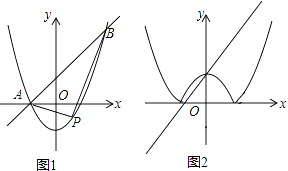
��1����ͼ1����k=1ʱ��ֱ��д��A��B��������ꣻ
��2���ڣ�1���������£���PΪ�������ϵ�һ�����㣬����ֱ��AB�·����������ABP��������ֵ����ʱ��P�����ꣻ
��3����ͼ2��������y=x2+��k��1��x��k��k��0����x�ύ�ڵ�C��D���㣨��C�ڵ�D����ࣩ����������x���·��IJ�����x�ᷭ�۵õ���ԭ������ʣ��IJ��������ͼ��ʾ��ͼ�Σ���ֱ��y=kx+1�����ͼ��ֻ�����������㣬�������ʱk��ȡֵ��Χ��
���𰸡�
��1��
�⣺��k=1ʱ�������ߵĽ���ʽΪy=x2��1��ֱ�ߵĽ���ʽΪy=x+1��
����ֱ���������ߣ��ã�
![]() ��
��
���x1=��1��x2=2��
��x=��1ʱ��y��x+1=0����x=2ʱ��y=x+1=3��
��A����1��0����B��2��3��
��2��
�⣺��P��x��x2��1������ͼ��
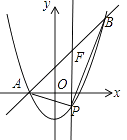
����P��PF��y�ᣬ��ֱ��AB��F��
��F��x��x+1����
PF=yF��yP=��x+1������x2��1��=��x2+x+2��
S��ABP=S��PFA+S��PFB= ![]() PF��xF��xA��+
PF��xF��xA��+ ![]() PF��xB��xF��
PF��xB��xF�� ![]() PF��
PF��
S��ABP= ![]() ����x2+x+2��=��
����x2+x+2��=�� ![]() ��x��
��x�� ![]() ��2+
��2+ ![]()
�ߵ�x= ![]() ʱ��yP=��
ʱ��yP=�� ![]() ��2��1=��
��2��1=�� ![]() ��
��
���ABP��������ֵΪ ![]() ��
��
��ʱ��P�����꣨ ![]() ����
���� ![]() ��
��
��3��
�⣺����ͼ��
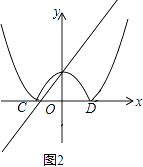
������y=0��
x2+��k��1��x��k=0��
������x+k����x��1��=0��
x=��k����x=1��
C����k��0����D��1��0����
ֱ��y=kx+1����0��1����
��������y=x2+��k��1��x��k����x��Գƣ�
�ã�y=��x2����k��1��x+k
����ֱ��y=kx+1���ã�
x2+��2k��1��x+1��k=0
��=��2k��1��2��4��1��k��=0
�ã�k= ![]() ���ᣩ��k=��
���ᣩ��k=�� ![]() ��
��
��k��0��
��0��k�� ![]() ��
��
��ֱ��y=kx+1������C����1��0��ʱ��k=1��
����ͼ���֪��0��k�� ![]() ��k��1ʱ��ֱ��y=kx+1�����ͼ��ֻ������������
��k��1ʱ��ֱ��y=kx+1�����ͼ��ֻ������������
����������1����k=1���������߽���ʽ��ֱ�߽���ʽ�����������飬�����������A��B�����ꣻ��2������P��y��ƽ���ߣ���������ABP�ָ������С�����Σ���PFΪ�ף������������θߵĺ�ΪAB�����ˮƽ���룬��������������������3����ͼ���۵������ֱ���뷭�ۺ�����������е���������������飬���kֵ�����k��0���������k��ȡֵ��Χ��
�����㾫�������ն��κ�����ͼ��Ͷ��κ����������ǽ����ĸ�������Ҫ֪�����κ���ͼ��ؼ��㣺1�����ڷ���2���Գ��� 3������ 4����x�ύ�� 5����y�ύ�㣻�����ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С��


 һŵ��ҵ�����ҵ���ּ�����������������ϵ�д�
һŵ��ҵ�����ҵ���ּ�����������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ACB=90�㣬��ABC=30�㣬����ABC�Ƶ�C˳ʱ����ת����A��B��C��ʹ��A��ǡ������AB�ϣ�����ת�Ƕ�Ϊ�� �� 
A.30��
B.45��
C.60��
D.90��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ֽ�е�ÿ��С�����DZ߳�Ϊ1����λ�������Σ��ڽ���ƽ��ֱ������ϵ��ABC�Ķ�����ڸ���ϣ���C������Ϊ��4����1����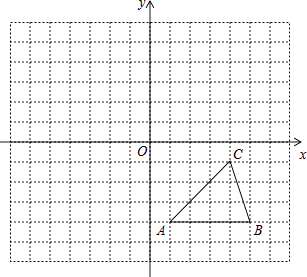
��1���ѡ�ABC����ƽ��5����λ��õ���Ӧ�ġ�A1B1C1 �� ������A1B1C1 �� ��д��C1�����꣮
��2���Ե�BΪλ�������ڸ�ֽ�ڻ�����A2BC2 �� �����ABC��λ�Ʊ�Ϊ2��1����д��C2�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���x2��2x+m��1=0������ʵ����x1 �� x2 ��
��1����m��ȡֵ��Χ��
��2����x12+x22=6x1x2ʱ����m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����ABO�Ƶ�A˳ʱ����ת����AB1C1��λ�ã���B��O�ֱ����ڵ�B1��C1������B1��x���ϣ��ٽ���AB1C1�Ƶ�B1˳ʱ����ת����A1B1C2��λ�ã���C2��x���ϣ�����A1B1C2�Ƶ�C2˳ʱ����ת����A2B2C2��λ�ã���A2��x���ϣ����ν�����ȥ��������A�� ![]() ��0����B��0��4�������B2014�ĺ�����Ϊ ��
��0����B��0��4�������B2014�ĺ�����Ϊ �� 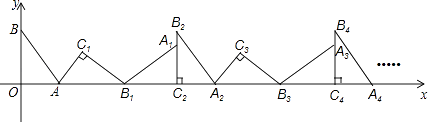
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڱ߳�Ϊa�����������ڵ�һ���߳�Ϊb��С�����Σ�a��b���������µIJ��ּ�ƴ��һ�����Σ���ͼ����ͨ������ͼ�Σ���Ӱ���֣����������֤��һ����ʽ���������ʽ�ǣ� ��
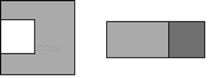
A. a2��b2=��a+b����a��b�� B. ��a+b��2=a2+2ab+b2
C. ��a��b��2=a2��2ab+b2 D. a2��ab=a��a��b��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������y=2x2��3ax+1�����Ա���x��ֵ����1��x��3������£������Ӧ�ĺ���ֵy����СֵΪ��23����a��ֵΪ�� ��
A.![]()
B.![]()
C.![]() ��
�� ![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪E��������ABCD�Խ���AC�ϵ�һ�㣬AE=AD������E��AC�Ĵ��ߣ�����CD�ڵ�F����FAD=�ȣ� 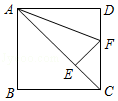
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ΪС�������ij���Ź�˾����һ֧MAT�ֻ������һ���źŵ����ַ������˹�˾ÿ������ȡͨ����������ѵķ�ʽ���£���ͨ���ѳ�������ѣ�ֻ��ͨ���ѣ���ͨ���Ѳ���������ѣ�ֻ������ѣ���С��ÿ���µ�ͨ���Ѿ�ΪxԪ��xΪ400��600֮������������ڲ������������ò�ʹ�����������£�x����Ϊ���ٲŻ�ʹ��ѡ���ҷ������ܻ��ѱȼ������ˣ���������
���� | �ҷ��� | |
�źŵ�����ѣ�Ԫ�� | 400 | 600 |
MAT�ֻ��۸�Ԫ�� | 15000 | 13000 |
ע��������Ϸ��������ڲ��ɱ������� | ||
A.500
B.516
C.517
D.600
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com