
【题目】如图,已知E是正方形ABCD对角线AC上的一点,AE=AD,过点E作AC的垂线,交边CD于点F,∠FAD=度. 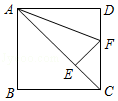
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=x2+(k﹣1)x﹣k与直线y=kx+1交于A,B两点,点A在点B的左侧.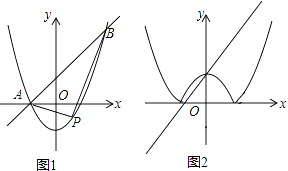
(1)如图1,当k=1时,直接写出A,B两点的坐标;
(2)在(1)的条件下,点P为抛物线上的一个动点,且在直线AB下方,试求出△ABP面积的最大值及此时点P的坐标;
(3)如图2,抛物线y=x2+(k﹣1)x﹣k(k>0)与x轴交于点C、D两点(点C在点D的左侧),抛物线在x轴下方的部分沿x轴翻折得到与原抛物线剩余的部分组成如图所示的图形,若直线y=kx+1与这个图形只有两个公共点,请求出此时k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购买60件A商品和30件B商品共用了1080元,购买50件A商品和20件B商品共用了880元
(1)A商品的单价是元,B商品的单价是元
(2)已知该商店购买B商品的件数比购买A商品的件数的2倍少4件,设购买A商品的件数为x件,该商店购买的A、B两种商品的总费用为y元 ①求y与x的函数关系式
②如果需要购买A、B两种商品的总件数不少于32件,且该商店购买的A、B两种商品的总费用不超过296元,求购买B商品最多有多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,过点(﹣2,3)的直线l经过一、二、三象限,若点(0,a),(﹣1,b),(c,﹣1)都在直线l上,则下列判断正确的是( )
A.a<b
B.a<3
C.b<3
D.c<﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点D为等腰直角△ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.
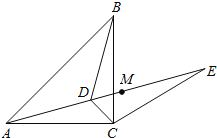
(1)求证:DE平分∠BDC;
(2)若点M在DE上,且DC=DM,求证:ME=BD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,梯子斜靠在与地面垂直(垂足为O)的墙上,当梯子位于AB位置时,它与地面所成的角∠ABO=60°;当梯子底端向右滑动1m(即BD=1m)到达CD位置时,它与地面所成的角∠CDO=45°,求梯子的长(结果保留根号) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是“经过已知直线外一点作这条直线的垂线”的尺规作图过程:
已知:直线l和l外一点P.(如图1)
求作:直线l的垂线,使它经过点P.
作法:如图2(1)在直线l上任取两点A,B;(2)分别以点A,B为圆心,AP,BP长为半径作弧,两弧相交于点Q;(3)作直线PQ.
所以直线PQ就是所求的垂线.
请回答:该作图的依据是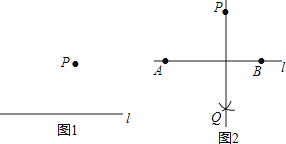
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com