
【题目】定义运算:ab=a(1﹣b).若a,b是方程x2﹣x+ ![]() m=0(m<0)的两根,则bb﹣aa的值为( )
m=0(m<0)的两根,则bb﹣aa的值为( )
A.0
B.1
C.2
D.与m有关
【答案】A
【解析】解:(方法一)∵a,b是方程x2﹣x+ ![]() m=0(m<0)的两根, ∴a+b=1,
m=0(m<0)的两根, ∴a+b=1,
∴bb﹣aa=b(1﹣b)﹣a(1﹣a)=b(a+b﹣b)﹣a(a+b﹣a)=ab﹣ab=0.
(方法二)∵a,b是方程x2﹣x+ ![]() m=0(m<0)的两根,
m=0(m<0)的两根,
∴a+b=1.
∵bb﹣aa=b(1﹣b)﹣a(1﹣a)=b﹣b2﹣a+a2=(a2﹣b2)+(b﹣a)=(a+b)(a﹣b)﹣(a﹣b)=(a﹣b)(a+b﹣1),a+b=1,
∴bb﹣aa=(a﹣b)(a+b﹣1)=0.
(方法三)∵a,b是方程x2﹣x+ ![]() m=0(m<0)的两根,
m=0(m<0)的两根,
∴a2﹣a=﹣ ![]() m,b2﹣b=﹣
m,b2﹣b=﹣ ![]() m,
m,
∴bb﹣aa=b(1﹣b)﹣a(1﹣a)=﹣(b2﹣b)+(a2﹣a)= ![]() m﹣
m﹣ ![]() m=0.
m=0.
故选A.
(方法一)由根与系数的关系可找出a+b=1,根据新运算找出bb﹣aa=b(1﹣b)﹣a(1﹣a),将其中的1替换成a+b,即可得出结论.
(方法二)由根与系数的关系可找出a+b=1,根据新运算找出bb﹣aa=(a﹣b)(a+b﹣1),代入a+b=1即可得出结论.
(方法三)由一元二次方程的解可得出a2﹣a=﹣ ![]() m、b2﹣b=﹣
m、b2﹣b=﹣ ![]() m,根据新运算找出bb﹣aa=﹣(b2﹣b)+(a2﹣a),代入后即可得出结论.
m,根据新运算找出bb﹣aa=﹣(b2﹣b)+(a2﹣a),代入后即可得出结论.


 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕点C顺时针旋转至△A′B′C,使点A′恰好落在AB上,则旋转角度为( ) 
A.30°
B.45°
C.60°
D.90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y= ![]() x2+bx+c的图象交x轴于A、D两点,并经过B点,已知A点坐标是(2,0),B点坐标是(8,6).
x2+bx+c的图象交x轴于A、D两点,并经过B点,已知A点坐标是(2,0),B点坐标是(8,6). 
(1)求二次函数的解析式;
(2)求函数图象的顶点坐标及D点的坐标;
(3)二次函数的对称轴上是否存在一点C,使得△CBD的周长最小?若C点存在,求出C点的坐标;若C点不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,AB=8cm,BC=16cm.点P从点A出发沿AB向点B以2cm/s的速度运动,点Q从点B出发沿BC向点C以4cm/s的速度运动.如果点P,Q分别从点A,B同时出发,则秒钟后△PBQ与△ABC相似? 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,﹣1).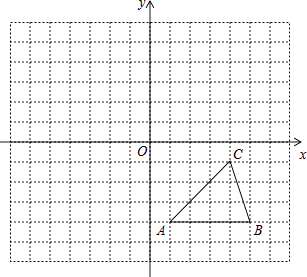
(1)把△ABC向上平移5个单位后得到对应的△A1B1C1 , 画出△A1B1C1 , 并写出C1的坐标.
(2)以点B为位似中心在格纸内画出△A2BC2 , 且与△ABC的位似比为2:1,并写出C2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣2x+m﹣1=0有两个实数根x1 , x2 .
(1)求m的取值范围;
(2)当x12+x22=6x1x2时,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com