
【题目】如图,梯子斜靠在与地面垂直(垂足为O)的墙上,当梯子位于AB位置时,它与地面所成的角∠ABO=60°;当梯子底端向右滑动1m(即BD=1m)到达CD位置时,它与地面所成的角∠CDO=45°,求梯子的长(结果保留根号) 
 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,﹣1).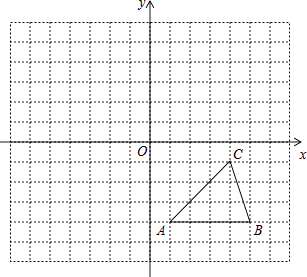
(1)把△ABC向上平移5个单位后得到对应的△A1B1C1 , 画出△A1B1C1 , 并写出C1的坐标.
(2)以点B为位似中心在格纸内画出△A2BC2 , 且与△ABC的位似比为2:1,并写出C2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果函数y=2x2﹣3ax+1,在自变量x的值满足1≤x≤3的情况下,与其对应的函数值y的最小值为﹣23,则a的值为( )
A.![]()
B.![]()
C.![]() 或
或 ![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游泳馆普通票价20元/张,暑假为了促销,新推出两种优惠卡: ①金卡售价600元/张,每次凭卡不再收费.
②银卡售价150元/张,每次凭卡另收10元.
暑假普通票正常出售,两种优惠卡仅限暑假使用,不限次数.设游泳x次时,所需总费用为y元
(1)分别写出选择银卡、普通票消费时,y与x之间的函数关系式;
(2)在同一坐标系中,若三种消费方式对应的函数图象如图所示,请求出点A、B、C的坐标;
(3)请根据函数图象,直接写出选择哪种消费方式更合算. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一块正方形和一块等腰直角三角形如图1摆放.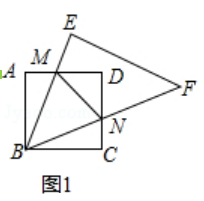
(1)如果把图1中的△BCN绕点B逆时针旋转90°,得到图2,则∠GBM=;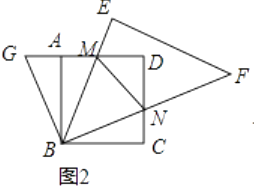
(2)将△BEF绕点B旋转.
①当M,N分别在AD,CD上(不与A,D,C重合)时,线段AM,MN,NC之间有一个不变的相等关系式,请你写出这个关系式:;(不用证明)
②当点M在AD的延长线上,点N在DC的延长线时(如图3),①中的关系式是否仍然成立?若成立,写出你的结论,并说明理由;若不成立,写出你认为成立的结论,并说明理由.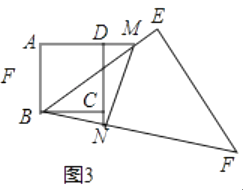
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2015年,中国女排获得第12届世界杯冠军,在女排训练中,甲、乙、丙三位队员进行战术演练,排球从一个队员随机传给另一个队员,每位传球队员传给其余两个队员的机会均等,但每位队员都不允许连续两次接触拍排球.现在要求经过两次传球(即经过一传、二传)后,第三次触球的队员再将排球扣到对方场地.
(1)若由甲开始第一次传球(即一传),经过第二次传球(即二传)后,最后排球还是由甲扣出的概率是多少?
(2)若三次触球都是随机的,求正好是甲、乙、丙分别承担一传、二传和扣球任务的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】表为小洁打算在某电信公司购买一支MAT手机与搭配一个门号的两种方案.此公司每个月收取通话费与月租费的方式如下:若通话费超过月租费,只收通话费;若通话费不超过月租费,只收月租费.若小洁每个月的通话费均为x元,x为400到600之间的整数,则在不考虑其他费用并使用两年的情况下,x至少为多少才会使得选择乙方案的总花费比甲方案便宜?( )
甲方案 | 乙方案 | |
门号的月租费(元) | 400 | 600 |
MAT手机价格(元) | 15000 | 13000 |
注意事项:以上方案两年内不可变更月租费 | ||
A.500
B.516
C.517
D.600
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系网格中,将△ABC进行位似变换得到△A1B1C1 . 
(1)△A1B1C1与△ABC的位似比是;
(2)画出△A1B1C1关于y轴对称的△A2B2C2;
(3)设点P(a,b)为△ABC内一点,则依上述两次变换后,点P在△A2B2C2内的对应点P2的坐标是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com