
【题目】将一块正方形和一块等腰直角三角形如图1摆放.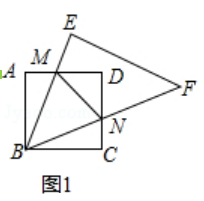
(1)如果把图1中的△BCN绕点B逆时针旋转90°,得到图2,则∠GBM=;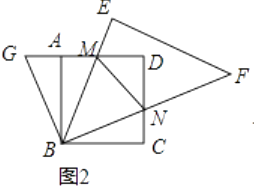
(2)将△BEF绕点B旋转.
①当M,N分别在AD,CD上(不与A,D,C重合)时,线段AM,MN,NC之间有一个不变的相等关系式,请你写出这个关系式:;(不用证明)
②当点M在AD的延长线上,点N在DC的延长线时(如图3),①中的关系式是否仍然成立?若成立,写出你的结论,并说明理由;若不成立,写出你认为成立的结论,并说明理由.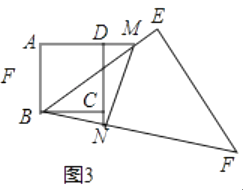
【答案】
(1)45°
(2)MN=AM+CN
【解析】解:(1)在正方形ABCD和等腰直角△BEF中,
∵∠ABC=90°,
∴∠EBF=45°,
∴∠ABM+∠CBN=45°,
由旋转的性质得∠GBA=∠CBN,
∴∠ABM+∠GBA=45°,
即∠GBM=45°,
所以答案是:45°;
⑵①AM+NC=MN;
理由:∵把图1中的△BCN绕点B逆时针旋转90°得到△ABG,
∴∠GAB=∠C=90°,AG=CN,BG=BN,∠ABG=∠CBN,
∴∠GAB+∠DAB=180°,
∴D,A,G三点共线,
∴∠ABM+∠GBA=45°,
∴∠GBM=∠MBN,
在△GBM与△NBM中, 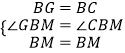 ,
,
∴△GBM≌△NBM,
∴GM=MN,
∵GM=AG+AM=CN+AM,
∴MN=AM+CN;
所以答案是:MN=AM+CN;
②上面的式子不成立,结论是:AM﹣NC=MN,
理由:在AM上截取AG,使得AG=CN,连结BG;
∵四边形ABCD是正方形,
∴AB=BC,∠A=∠BCN=90°,
在△BAG与△BCN中, 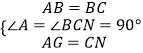 ,
,
∴△BAG≌△BCN,
∴BG=BN,∠ABG=∠NBC,
∴∠MBN=∠MBC+∠CBN=∠MBC+∠ABG=45°=∠GBM,
在△BGM与△BMN中,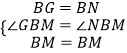 ,
,
∴△BGM≌△BNM,
∴GM=NM,
∴AM﹣CN=MN.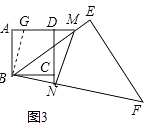
【考点精析】本题主要考查了正方形的性质和旋转的性质的相关知识点,需要掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形;①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】某商店购买60件A商品和30件B商品共用了1080元,购买50件A商品和20件B商品共用了880元
(1)A商品的单价是元,B商品的单价是元
(2)已知该商店购买B商品的件数比购买A商品的件数的2倍少4件,设购买A商品的件数为x件,该商店购买的A、B两种商品的总费用为y元 ①求y与x的函数关系式
②如果需要购买A、B两种商品的总件数不少于32件,且该商店购买的A、B两种商品的总费用不超过296元,求购买B商品最多有多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点D为等腰直角△ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.
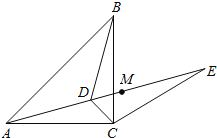
(1)求证:DE平分∠BDC;
(2)若点M在DE上,且DC=DM,求证:ME=BD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,梯子斜靠在与地面垂直(垂足为O)的墙上,当梯子位于AB位置时,它与地面所成的角∠ABO=60°;当梯子底端向右滑动1m(即BD=1m)到达CD位置时,它与地面所成的角∠CDO=45°,求梯子的长(结果保留根号) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形A1B1C1O,A2B2C2C1 , A3B3C3C2 , …按如图的方式放置.点A1 , A2 , A3 , …和点C1 , C2 , C3 , …分别在直线y=x+1和x轴上,则点B6的坐标是 . 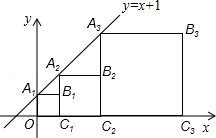
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.小明计划给朋友快递一部分物品,经了解有甲、乙两家快递公司比较合适.甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费.乙公司表示:按每千克16元收费,另加包装费3元.设小明快递物品x千克.
(1)请分别写出甲、乙两家快递公司快递该物品的费用y(元)与x(千克)之间的函数关系式;
(2)小明选择哪家快递公司更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究:
①新知学习
若把将一个平面图形分为面积相等的两个部分的直线叫做该平面图形的“面线”,其“面线”被该平面图形截得的线段叫做该平面图形的“面径”(例如圆的直径就是圆的“面径”).
②解决问题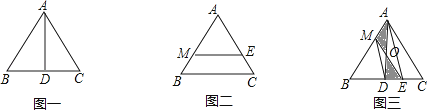
已知等边三角形ABC的边长为2.
(1)如图一,若AD⊥BC,垂足为D,试说明AD是△ABC的一条面径,并求AD的长;
(2)如图二,若ME∥BC,且ME是△ABC的一条面径,求面径ME的长;
(3)如图三,已知D为BC的中点,连接AD,M为AB上的一点(0<AM<1),E是DC上的一点,连接ME,ME与AD交于点O,且S△MOA=S△DOE .
①求证:ME是△ABC的面径;
②连接AE,求证:MD∥AE;
(4)请你猜测等边三角形ABC的面径长l的取值范围(直接写出结果)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com