
【题目】如图,已知点D为等腰直角△ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.
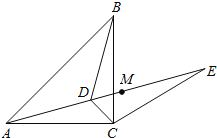
(1)求证:DE平分∠BDC;
(2)若点M在DE上,且DC=DM,求证:ME=BD.
【答案】(1)证明见解析;(2)证明见解析
【解析】
试题分析:(1)根据△ABC是等腰直角三角形得出∠BAC=∠ABC=45°,根据∠CAD=∠CBD=15°得出∠BAD=∠ABD=30°,则BD=AD,说明D在AB的垂直平分线上,根据AC=BC得出点C也在AB的垂直平分线上,从而说明直线CD是AB的垂直平分线,则∠ACD=∠BCD=45°,∠CDE=∠BDE=60°,即DE平分∠BDC;(2)连接MC,根据DC=DM,∠MDC=60°得到△MDC为正三角形,则CM=CD,∠DMC=∠MDC=60°,从而得到∠DAC=∠CEM,从而说明△ADC和△EMC全等,则ME=AD=BD.
试题解析:(1)∵△ABC是等腰直角三角形, ∴∠BAC=∠ABC=45°, ∵∠CAD=∠CBD=15°,
∴∠BAD=∠ABD=45°﹣15°=30°, ∠ABD=∠ABC﹣15°=30°, ∴∠BAD=∠ABD ∴BD=AD,
∴D在AB的垂直平分线上, ∵AC=BC, ∴C也在AB的垂直平分线上, 即直线CD是AB的垂直平分线,
∴∠ACD=∠BCD=45°, ∴∠CDE=15°+45°=60°, ∴∠BDE=∠DBA+∠BAD=60°; ∴∠CDE=∠BDE,
即DE平分∠BDC.
(2)如图,连接MC.
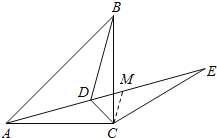
∵DC=DM,且∠MDC=60°, ∴△MDC是等边三角形,
∴CM=CD.∠DMC=∠MDC=60°, ∵∠ADC+∠MDC=180°,∠DMC+∠EMC=180°, ∴∠EMC=∠ADC.
又∵CE=CA, ∴∠DAC=∠CEM.
在△ADC与△EMC中,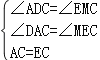 , ∴△ADC≌△EMC(AAS), ∴ME=AD=BD.
, ∴△ADC≌△EMC(AAS), ∴ME=AD=BD.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,把点A(x,2)向上平移3个单位长度,再向右平移2个单位长度得到点B(-3,y),则x和y分别为( )
A. -6,-4 B. -1,5 C. -5,3 D. -5,5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列因式分解正确的是( )
A. x2﹣y2=(x﹣y)2 B. xy﹣x=x(y﹣1)
C. a2+a+1=(a+1)2 D. 2x+y=2(x+y)
查看答案和解析>>
科目:初中数学 来源: 题型:
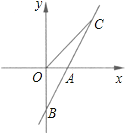
【题目】如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,﹣2).
(1)求直线AB的解析式;
(2)若直线AB上的点C在第一象限,且S△BOC=2,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】增强公民的节约意识,合理利用天然气资源,某市自1月1日起对市区民用管道天然气价格进行调整,实行阶梯式气价,调整后的收费价格如表所示:
每月用气量 | 单价(元/m3) |
不超出75m3的部分 | 2.5 |
超出75m3不超出125m3的部分 | a |
超出125m3的部分 | a+0.25 |
(1)若甲用户3月份的用气量为60m3,则应缴费 元;
(2)若调价后每月支出的燃气费为y(元),每月的用气量为x(m3),y与x之间的关系如图所示,求a的值及y与x之间的函数关系式;

(3)在(2)的条件下,若乙用户2、3月份共用1气175m3(3月份用气量低于2月份用气量),共缴费455元,乙用户2、3月份的用气量各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
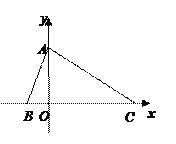
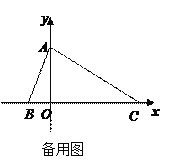
【题目】如图,在平面直角坐标系中,点A、B、C的坐标分别为(0,2)、(-1,0)、(4,0).P是线段BC上的一动点(点P与点B、C不重合),假设p的横坐标是t.过点P的直线与直线y=x平行且与AC相交于点Q.设△QPC关于直线PQ的对称的图形与四边形ABPQ重叠部分的面积为S.
⑴点C关于直线PQ的对称点C′的坐标为________;
⑵△ABC是什么三角形?为什么?
(3)求S与t的函数关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,并且关于x的一元二次方程ax2+bx+c﹣m=0有两个不相等的实数根,下列结论:
①b2﹣4ac<0;②abc>0;③a﹣b+c<0;④m>﹣2,
其中,正确的个数有( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABC的顶点分别为A(-4, 5),B(﹣3, 2),C(4,-1).
⑴作出△ABC关于x轴对称的图形△A1B1C1;
⑵写出A1、B1、C1的坐标;
⑶若AC=10,求△ABC的AC边上的高.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com