
【题目】增强公民的节约意识,合理利用天然气资源,某市自1月1日起对市区民用管道天然气价格进行调整,实行阶梯式气价,调整后的收费价格如表所示:
每月用气量 | 单价(元/m3) |
不超出75m3的部分 | 2.5 |
超出75m3不超出125m3的部分 | a |
超出125m3的部分 | a+0.25 |
(1)若甲用户3月份的用气量为60m3,则应缴费 元;
(2)若调价后每月支出的燃气费为y(元),每月的用气量为x(m3),y与x之间的关系如图所示,求a的值及y与x之间的函数关系式;

(3)在(2)的条件下,若乙用户2、3月份共用1气175m3(3月份用气量低于2月份用气量),共缴费455元,乙用户2、3月份的用气量各是多少?
【答案】解:(1)150。
(2)由题意,得![]() ,∴a+0.25=3。
,∴a+0.25=3。
设OA的解析式为y1=k1x,则有2.5×75=75k1,∴k1=2.5。
∴线段OA的解析式为y1=2.5x(0≤x≤75)。
设线段AB的解析式为y2=k2x+b,由图象,得
![]() ,解得:
,解得:![]() 。
。
∴线段AB的解析式为:![]() (75<x≤125)。
(75<x≤125)。
∵(385﹣325)÷3=20,∴C(145,385)。
设射线BC的解析式为y3=k3x+b1,由图象,得
![]() ,解得:
,解得:![]() 。
。
∴射线BC的解析式为![]() (x>125)。
(x>125)。
综上所述,y与x之间的函数关系式为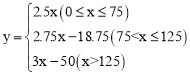 。
。
(3)设乙用户2月份用气xm3,则3月份用气(175﹣x)m3,
当x>125,175﹣x≤75时,3x﹣50+2.5(175﹣x)=455,
解得:x=135,175﹣135=40,符合题意;
当75<x≤125,175﹣x≤75时,2.75x﹣18.75+2.5(175﹣x)=455,
解得:x=145,不符合题意,舍去;
当75<x≤125,75<175﹣x≤125时,2.75x﹣18.75+2.75(175﹣x)=455,此方程无解.
∴乙用户2、3月份的用气量各是135m3,40m3。
【解析】(1)根据单价×数量=总价就可以求出3月份应该缴纳的费用:60×2.5=150(元)。
(2)结合统计表的数据,根据单价×数量=总价的关系建立方程就可以求出a值,再从0≤x≤75,75<x≤125和x>125运用待定系数法分别表示出y与x的函数关系式即可。
(3)设乙用户2月份用气xm3,则3月份用气(175﹣x)m3,分3种情况:x>125,175﹣x≤75时,75<x≤125,175﹣x≤75时,当75<x≤125,75<175﹣x≤125时分别建立方程求出其解即可。


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】现有以下五个结论:①0没有相反数;②若两个数互为相反数,则它们相除的商等于-1;③负数的绝对值是它的倒数;④绝对值等于其本身的有理数是零;⑤几个有理数相乘,负因数个数为奇数则乘积为负数.其中正确的有( )
A.0个B.1个C.2个D.3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在梯形ABCD中,AD∥BC,∠B=90°,AB=14cm,AD=18cm,BC=21cm,点P从点A开始沿AD边向点D以1cm/秒的速度移动,点Q从点C开始沿CB边向点B以2cm/秒的速度移动.如果P、Q分别从A、C同时出发.设移动的时间为t.
求:(1)t为何值时,梯形PQCD是等腰梯形;
(2)t为何值时,AB的中点E到线段PQ的距离为7cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点D为等腰直角△ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.
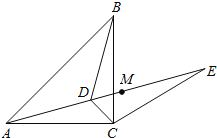
(1)求证:DE平分∠BDC;
(2)若点M在DE上,且DC=DM,求证:ME=BD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一批衬衫,平均每天可售出20件,每件盈利40元,为了扩大销售,增加利润,尽量减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫降价1元,商场平均每天可多售出2件,若商场每天要获利润1200元,请计算出每件衬衫应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D在BC上,BD=DC,过点D作DE⊥AC,垂足为E,⊙O经过A,B,D三点.
(1)求证:AB是⊙O的直径;
(2)判断DE与⊙O的位置关系,并加以证明;
(3)若⊙O的半径为3,∠BAC=60°,求DE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com