
【题目】已知:如图,在梯形ABCD中,AD∥BC,∠B=90°,AB=14cm,AD=18cm,BC=21cm,点P从点A开始沿AD边向点D以1cm/秒的速度移动,点Q从点C开始沿CB边向点B以2cm/秒的速度移动.如果P、Q分别从A、C同时出发.设移动的时间为t.
求:(1)t为何值时,梯形PQCD是等腰梯形;
(2)t为何值时,AB的中点E到线段PQ的距离为7cm.

【答案】(1)8秒;(2)t=3.5或t=7
【解析】试题分析:(1)过P作PN⊥BC于N,过D作DM⊥BC于M,先证明四边形ABMD是矩形,从而得到AD=BM,再根据边与边之间的关系,列一元一次方程3t﹣21=3,得到t=8,即t=8秒时,梯形PQCD是等腰梯形;
(2)在Rt△PQM中,表示出PM=14,QM=3t﹣1,然后根据PM2+QM2=PQ2,得到142+(3t﹣21)2=(21﹣t)2,求得t值即可.
试题解析:
如图1,过P作PN⊥BC于N,过D作DM⊥BC于M,
∵AD∥BC,∠B=90°,DM⊥BC,
∴四边形ABMD是矩形,AD=BM.
∴MC=BC﹣BM=BC﹣AD=3.
又∵QN=BN﹣BQ=AP﹣BQ=t﹣(21﹣2t)=3t﹣21.
若梯形PQCD为等腰梯形,则QN=MC=3.
得3t﹣21=3,t=8,
即t=8秒时,梯形PQCD是等腰梯形.
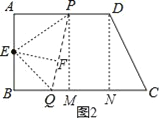
(2)如图2,过E作EF⊥PQ于F,连接PE,EQ,当EF=7cm时,
∵AE=BE=![]() AB=
AB=![]() ×14=7cm,
×14=7cm,
∴AE=EF=BE,
∵AD∥BC,∠B=90°,
∴∠A=90°,
∵PE=PE,EQ=EQ,
∴△AEP≌△FEP,△BEQ≌△FEQ,
∴PA=PF=t,BQ=FQ=21﹣2t,
∴PQ=PF+FQ=21﹣t,
在Rt△PQM中,PM=14,QM=3t﹣1,
∵PM2+QM2=PQ2,
∴142+(3t﹣21)2=(21﹣t)2,
解得:t=3.5或t=7,
∴当t为3.5或7时,AB的中点E到线段PQ的距离为7cm.



 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣![]() x+8与x轴、y轴分别相交于点A、B,设M是OB上一点,若将△ABM沿AM折叠,使点B恰好落在x轴上的点B′处.求:
x+8与x轴、y轴分别相交于点A、B,设M是OB上一点,若将△ABM沿AM折叠,使点B恰好落在x轴上的点B′处.求:
(1)点B′的坐标;
(2)直线AM所对应的函数关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系中,等腰Rt△ABC的顶点A、C在坐标轴上运动,且∠ACB=90°,AC=BC.
(1)如图1,当A(0,-2),C(1,0),点B在第四象限时,则点B的坐标为_____;
(2)如图2,当点C在x轴正半轴上运动,点A在y轴正半轴上运动,点B在第四象限时,作BD⊥y轴于点D,试判断![]() 与
与![]() 哪一个是定值,并说明定值是多少?请证明你的结论.
哪一个是定值,并说明定值是多少?请证明你的结论.
(3)如图3,当点C在y轴正半轴上运动,点A在x轴正半轴上运动,使点D恰为BC的中点,连接DE,求证:∠ADC=∠BDE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,把点A(x,2)向上平移3个单位长度,再向右平移2个单位长度得到点B(-3,y),则x和y分别为( )
A. -6,-4 B. -1,5 C. -5,3 D. -5,5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若10m=5,10n=3,则102m+3n= .
【答案】675.
【解析】102m+3n=102m103n=(10m)2(10n)3=5233=675,
故答案为:675.
点睛:此题考查了幂的乘方与积的乘方, 同底数幂的乘法. 首先根据同底数幂的乘法法则,可得102m+3n=102m×103n,然后根据幂的乘方的运算方法,可得102m×103n=(10m)2×(10n)3,最后把10m=5,10n=2代入化简后的算式,求出102m+3n的值是多少即可.
【题型】填空题
【结束】
18
【题目】计算:
(1)(5mn2﹣4m2n)(﹣2mn)
(2)(x+7)(x﹣6)﹣(x﹣2)(x+1)
(3) (-![]() )2 016×161 008;
)2 016×161 008;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列因式分解正确的是( )
A. x2﹣y2=(x﹣y)2 B. xy﹣x=x(y﹣1)
C. a2+a+1=(a+1)2 D. 2x+y=2(x+y)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】增强公民的节约意识,合理利用天然气资源,某市自1月1日起对市区民用管道天然气价格进行调整,实行阶梯式气价,调整后的收费价格如表所示:
每月用气量 | 单价(元/m3) |
不超出75m3的部分 | 2.5 |
超出75m3不超出125m3的部分 | a |
超出125m3的部分 | a+0.25 |
(1)若甲用户3月份的用气量为60m3,则应缴费 元;
(2)若调价后每月支出的燃气费为y(元),每月的用气量为x(m3),y与x之间的关系如图所示,求a的值及y与x之间的函数关系式;

(3)在(2)的条件下,若乙用户2、3月份共用1气175m3(3月份用气量低于2月份用气量),共缴费455元,乙用户2、3月份的用气量各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】互联网“微商”经营已成为大众创业新途径,某微信平台上一件商品标价为200元,按标价的五折销售,仍可获利20元,则这件商品的进价为
A.120元
B.100元
C.80元
D.60元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com