
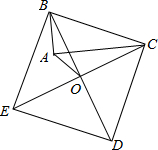
 如图,以Rt△ABC的斜边BC为一边作正方形BCDE,设正方形的中心为O,连结AO,如果AB=3,AO=2$\sqrt{2}$,那么AC的长为7.
如图,以Rt△ABC的斜边BC为一边作正方形BCDE,设正方形的中心为O,连结AO,如果AB=3,AO=2$\sqrt{2}$,那么AC的长为7. 分析 如图在CA上截取CM=AB,连接OM,只要证明△ABO≌△MCO得△OAM是等腰直角三角形,求出AM即可解决问题.
解答 解: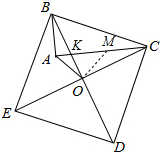 如图在CA上截取CM=AB,连接OM,
如图在CA上截取CM=AB,连接OM,
∵四边形BCDE是正方形,
∴OB=OC,∠BOC=90°,
∵∠ABO+∠AKB=90°,∠OCM+∠OKC=90°,∠AKB=∠OKC,
∴∠ABO=∠OCM,
在△ABO和△MCO中,
$\left\{\begin{array}{l}{AB=CM}\\{∠ABO=∠MCO}\\{BO=CO}\end{array}\right.$,
∴△ABO≌△MCO,
∴AO=MO,∠AOB=∠COM,
∴∠AOM=∠BOC=90°,
∵AO=OM=2$\sqrt{2}$,AB=CM=3,
∴AM=$\sqrt{A{O}^{2}+{MO}^{2}}$=4,
∴AC=AM+CM=4+3=7
故答案为:7.
点评 本题考查全等三角形的判定和性质、正方形的性质、勾股定理等知识.解题的关键是添加辅助线构造全等三角形,属于中考常考题型.


科目:初中数学 来源: 题型:填空题
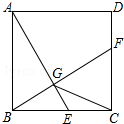 如图,已知正方形ABCD的边长为1,E是边BC上的动点,BF⊥AE交CD于点F,垂足为G,连结CG.下列说法:
如图,已知正方形ABCD的边长为1,E是边BC上的动点,BF⊥AE交CD于点F,垂足为G,连结CG.下列说法:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
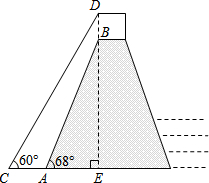 我国南水北调中线工程的起点是丹江水库,按照工程计划,需对原水库大坝进行混凝土加高,使坝高由原来的162米增加到173米,以抬高蓄水位.如图是某一段坝体加高工程的截面示意图,其中原坝体的高为B,背水坡坡角∠BAE=68°,新坝体的高为DE,背水坡坡角∠DCE=60°.求工程完工后背水坡坡底端水平方向增加的宽度AC.
我国南水北调中线工程的起点是丹江水库,按照工程计划,需对原水库大坝进行混凝土加高,使坝高由原来的162米增加到173米,以抬高蓄水位.如图是某一段坝体加高工程的截面示意图,其中原坝体的高为B,背水坡坡角∠BAE=68°,新坝体的高为DE,背水坡坡角∠DCE=60°.求工程完工后背水坡坡底端水平方向增加的宽度AC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com