
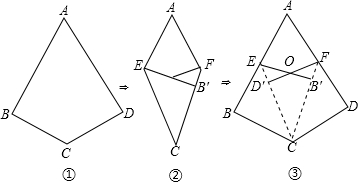
分析 (1)根据“完美风筝”的定义判断即可得到结果;
(2)根据对折得到∠BCD′=∠B′EC′=$\frac{1}{3}$∠BCD=40°,再由三角形的内角和,和邻补角即可;
(3)根据“完美筝形”的定义得出线段、角相等,转化到四边形OD′CB′中,即可.
解答 解:(1)∵四边形ABCD是正方形,
∴AB=AD,CB=CD,∠B=∠D=90°,
∴完美筝形”
故答案为正方形;
(2)由对折有,∠BEC=∠B′EC,
∵∠BCD′=∠ECF=∠FCD,且∠BCD=120°,
∴∠BCD′=$\frac{1}{3}$∠BCD=40°,
∴∠CBE=90°-∠BCD′=50°,
∴∠BEB′=100°
∴∠AEB′=80°,
故答案为80°.
(3)四边形ODCB是“完美筝形”
理由如下:
∵四边形ABCD是“完美筝形”,
∴AB=AD,CB=CD,∠B=∠D=90°,
∴CD′=CB′,∠CD′O=∠CB′O=90°,
∴∠ED′O=∠FB′O=90°,
∵四边形AECF为菱形,
∴CE=CF,
∴D′E=B′F,
∵∠EOD′=∠FOB′,
∴△EOD′≌△FOB′,
∴OD′=OB′,
∴四边形OD′CB′是“完美筝形”
点评 此题是四边形的综合题,主要考查了特殊平行四边形的性质和判定,解本题的关键是“完美筝形”的定义的条件,难点是对折中找出相等量.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:解答题
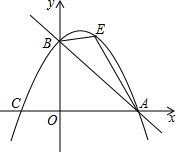 如图,在平面直角坐标系中,直线y=-$\frac{3}{4}$x+3与x轴交于点A,与y轴交于点B.抛物线y=ax2+$\frac{3}{4}x+c$经过A、B两点,点E是直线AB上方抛物线上的一点.
如图,在平面直角坐标系中,直线y=-$\frac{3}{4}$x+3与x轴交于点A,与y轴交于点B.抛物线y=ax2+$\frac{3}{4}x+c$经过A、B两点,点E是直线AB上方抛物线上的一点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
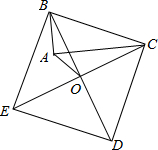 如图,以Rt△ABC的斜边BC为一边作正方形BCDE,设正方形的中心为O,连结AO,如果AB=3,AO=2$\sqrt{2}$,那么AC的长为7.
如图,以Rt△ABC的斜边BC为一边作正方形BCDE,设正方形的中心为O,连结AO,如果AB=3,AO=2$\sqrt{2}$,那么AC的长为7.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
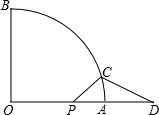 如图,线段PA=1,点D是线段PA延长线上的点,AD=a(a>1),点O是线段AP延长线上的点,OA2=OP•OD,以O为圆心,OA为半径作扇形OAB,∠BOA=90°.
如图,线段PA=1,点D是线段PA延长线上的点,AD=a(a>1),点O是线段AP延长线上的点,OA2=OP•OD,以O为圆心,OA为半径作扇形OAB,∠BOA=90°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
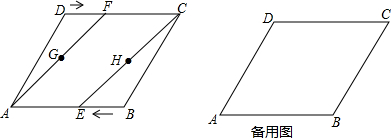
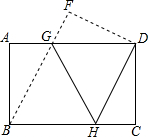 将矩形纸片ABCD如图折叠,使点B与点D重合,折痕为GH.
将矩形纸片ABCD如图折叠,使点B与点D重合,折痕为GH.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com