
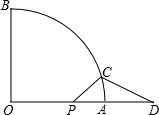
 如图,线段PA=1,点D是线段PA延长线上的点,AD=a(a>1),点O是线段AP延长线上的点,OA2=OP•OD,以O为圆心,OA为半径作扇形OAB,∠BOA=90°.
如图,线段PA=1,点D是线段PA延长线上的点,AD=a(a>1),点O是线段AP延长线上的点,OA2=OP•OD,以O为圆心,OA为半径作扇形OAB,∠BOA=90°.分析 (1)如图1中,连接OE,作OM⊥BC于M.设⊙O半径为r,先列出关于r的方程求出r,再求出OM,在RT△BOM中利用勾股定理即可.
(2)如图2中,⊙C与⊙P相切于点M,连接DM与⊙P交于点Q,连接PQ、CQ、OC,想分别证明点A是△CMD的重心即可.
(3)如图3中,连接OC、PB、AC,想办法证明△OBC是等边三角形,再利用方程即可解决问题.
解答 解:(1)如图1中,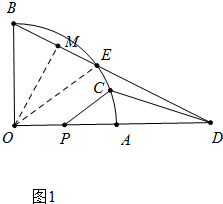 连接OE,作OM⊥BC于M.设⊙O半径为r,
连接OE,作OM⊥BC于M.设⊙O半径为r,
∵OA2=OP•OD,
∴r2=(r-1)(r+2),
∴r=2,
在RT△BOD中,∵OB=2,OD=4,
∴BD=$\sqrt{B{O}^{2}+O{D}^{2}}$=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,
∵$\frac{1}{2}$•OD•OB=$\frac{1}{2}$•BD•OM,
∴OM=$\frac{4\sqrt{5}}{5}$,
在RT△BOM中,∵$BO=2,OM=\frac{4\sqrt{5}}{5}$,
∴BM=$\sqrt{O{B}^{2}-O{M}^{2}}$=$\frac{2\sqrt{5}}{5}$,
∵OM⊥BE,
∴BM=ME,BE=2BM=$\frac{4\sqrt{5}}{5}$.
(2)如图2中,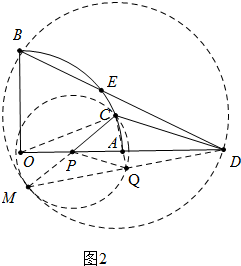 ⊙C与⊙P相切于点M,连接DM与⊙P交于点Q,连接PQ、CQ、OC.
⊙C与⊙P相切于点M,连接DM与⊙P交于点Q,连接PQ、CQ、OC.
∵OA2=OP•OD,
∴OC2=OP•OD,
∴$\frac{OC}{OP}$=$\frac{OD}{OP}$,
∵∠COP=∠DOC,
∴△COP∽△DOC,
∴∠OCP=ODC,
∵OC=OA,
∴∠OCA=∠OAC,
∴∠OCP+∠PCA=∠ACD+∠ODC,
∴∠PCA=∠DCA,
∵CM=CD,∠CQM=90°(直径CM所对的圆周角是直角),
∴∠MCQ=∠DCQ,
∴C、A、Q共线,
∵MP=PC,MQ=QD,
∴PQ∥CD,PQ=$\frac{1}{2}$CD,
∴PA:AD=PQ:CD=1:2,
∴AD=2PA=2.
(3)如图3中,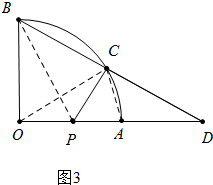 连接OC、PB、AC.
连接OC、PB、AC.
∵∵OA2=OP•OD,
∴OC2=OP•OD,
∴$\frac{OC}{OP}$=$\frac{OD}{OP}$,
∵∠COP=∠DOC,
∴△COP∽△DOC,
∴∠OCP=ODC,
同理△BOP∽△DOB,∠OBP=∠D,
∴∠OBP=∠OCP,
∴O、B、C、P四点共圆,
∴∠BOP+∠BCP=90°,
∵PC•OA=BC•OP,
∴$\frac{PC}{OP}$=$\frac{BC}{BO}$,∵∠BOP=∠BCP,
∴△PBO∽△PBC,
∴$\frac{PC}{OP}$=$\frac{BC}{BO}$=$\frac{PB}{PB}$=1,
∴OB=BC=OC,PC=OP,设BO=BC=OC=r,
∴△BOC是等边三角形,
∴∠OBC=60°,∠D=30°,
在RT△PCD中,∵PC=OP=r-1,
∴PD=2PC=2r-2,
∴AD=2r-3,
∵OD=$\sqrt{3}$OB,
∴r+2r-3=$\sqrt{3}$r,
∴r=$\frac{{3+\sqrt{3}}}{2}$,
∴扇形OAB的半径长为$\frac{3+\sqrt{3}}{2}$.
点评 本题考查圆的有关性质、相似三角形的判定和性质、勾股定理、四点共圆等知识,解题的关键是添加辅助线构造相似三角形,学会用面积法求三角形的高,把问题转化为方程去思考,掌握用特殊三角形解决问题的思想方法,属于中考压轴题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | P>Q | B. | P=Q | C. | P<Q | D. | 不能确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com