
【题目】如图,一次函数y=kx+b与反比例函数![]() 的图象交于A(m,6),B(3,n)两点.
的图象交于A(m,6),B(3,n)两点.
(1)求一次函数的解析式;
(2)根据图象直接写出![]() 的x的取值范围;
的x的取值范围;
(3)求△AOB的面积.

【答案】(1)y=-2x+8;(2)0<x<1或x>3.(3)8.
【解析】试题分析:(1)先根据反比例函数图象上点的坐标特征得到6m=6,3n=6,解得m=1,n=2,这样得到A点坐标为(1,6),B点坐标为(3,2),然后利用待定系数求一次函数的解析式;
(2)观察函数图象找出反比例函数图象都在一次函数图象上方时x的取值范围;
(3)先确定一次函数图象与坐标轴的交点坐标,然后利用S△AOB=S△COD-S△COA-S△BOD进行计算.
试题解析:(1)分别把A(m,6),B(3,n)代入![]() (x>0)得6m=6,3n=6,
(x>0)得6m=6,3n=6,
解得m=1,n=2,
所以A点坐标为(1,6),B点坐标为(3,2),
分别把A(1,6),B(3,2)代入y=kx+b得![]() ,
,
解得![]() ,
,
所以一次函数解析式为y=-2x+8;
(2)当0<x<1或x>3时, ![]() ;
;
(3)如图,
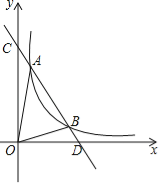
当x=0时,y=-2x+8=8,则C点坐标为(0,8),
当y=0时,-2x+8=0,解得x=4,则D点坐标为(4,0),
所以S△AOB=S△COD-S△COA-S△BOD
=![]() ×4×8-
×4×8-![]() ×8×1-
×8×1-![]() ×4×2
×4×2
=8.


科目:初中数学 来源: 题型:
【题目】甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地距离y(千米)与x(小时)之间的函数关系.请根据图象解答下列问题:
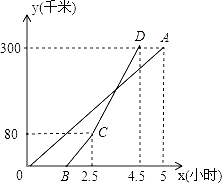
(1)轿车到达乙地后,货车距乙地多少千米?
(2)求线段CD对应的函数解析式.
(3)轿车到达乙地后,马上沿原路以CD段速度返回,求货车从甲地出发后多长时间再与轿车相遇(结果精确到0.01).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】校学生会体育部为更好的开展同学们课外体育活动,现对学生最喜欢的一项球类运动进行了随机抽样调查,根据调查的结果绘制成如图①和②所示的两幅不完整的统计图,其中 A.喜欢篮球 B.喜欢足球 C.喜欢乒乓球,D.喜欢排球,请你根据统计图提供的信息,完成下列问题:

(1)本次一共调查了 名学生;
(2)把图①汇总条形统计图补充完整;
(3)求图②中表示“D.喜欢排球”部分所在扇形的圆心角的度数;
(4)若该校有3000名学生,请你估计全校可能有多少名学生喜欢足球运动.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列图形中,是轴对称图形的有( )
①正方形; ②菱形; ③矩形; ④平行四边形; ⑤等腰三角形; ⑥直角三角形
A. 6个B. 5个C. 4个D. 3个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com