
分析 根据二次根式的性质和分式的意义,被开方数大于或等于0,分母不等于0,可以求出x的范围.
解答 解:由$\sqrt{2x+3}$+$\frac{1}{x+1}$在实数范围内有意义,得
$\left\{\begin{array}{l}{2x+3≥0}\\{x+1≠0}\end{array}\right.$,
解得-$\frac{3}{2}$≤x<-1或x>-1,
故答案为:-$\frac{3}{2}$≤x<-1或x>-1.
点评 本题考查了二次根式有意义的条件,当函数表达式是整式时,自变量可取全体实数;当函数表达式是分式时,考虑分式的分母不能为0;当函数表达式是二次根式时,被开方数非负.


 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:选择题
| A. | y=0.2x+0.1 | B. | y=0.1x | C. | y=0.1x-0.1 | D. | y=0.1x+0.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
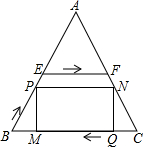 如图,在等边三角形ABC中,BC=180,E,F分别是AB,AC的中点,点P从点B出发,沿折线段BE-EF以每秒6个单位长的速度向点F匀速运动,点Q从点C出发沿线段CB方向以每秒3个单位长的速度向点B匀速运动,点P,Q同时出发,当点P与点F重合时点P停止运动,点Q也随之停止,设点P的运动时间为t秒.
如图,在等边三角形ABC中,BC=180,E,F分别是AB,AC的中点,点P从点B出发,沿折线段BE-EF以每秒6个单位长的速度向点F匀速运动,点Q从点C出发沿线段CB方向以每秒3个单位长的速度向点B匀速运动,点P,Q同时出发,当点P与点F重合时点P停止运动,点Q也随之停止,设点P的运动时间为t秒.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com