
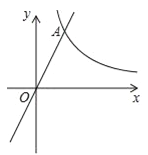
【题目】已知:如图,在平面直角坐标系xOy中,反比例函数![]() 的图象与正比例函数y=kx(k≠0)的图象相交于横坐标为2的点A,平移直线OA,使它经过点B(3,0),与y轴交于点C.
的图象与正比例函数y=kx(k≠0)的图象相交于横坐标为2的点A,平移直线OA,使它经过点B(3,0),与y轴交于点C.
(1)求平移后直线的表达式;
(2)求∠OBC的余切值.
【答案】(1)y=2x﹣6;(2)![]() .
.
【解析】
试题分析:(1)根据点A在反比例函数图象上可求出点A的坐标,进而可求出正比例函数表达式,根据平移的性质可设直线BC的函数解析式为y=2x+b,根据点B的坐标利用待定系数法即可求出b值,此题得解;
(2)利用一次函数图象上点的坐标特征即可求出点C的坐标,从而得出OC的值,再根据余切的定义即可得出结论.
试题解析:(1)当x=2时,y=![]() =4,∴点A的坐标为(2,4).
=4,∴点A的坐标为(2,4).
∵A(2,4)在y=kx(k≠0)的图象上,∴4=2k,解得:k=2.
设直线BC的函数解析式为y=2x+b,∵点B的坐标为(3,0),∴0=2×3+b,解得:b=﹣6,∴平移后直线的表达式y=2x﹣6.
(2)当x=0时,y=﹣6,∴点C的坐标为(0,﹣6),∴OC=6,∴cot∠OBC=![]() =
=![]() =
=![]() .
.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:初中数学 来源: 题型:
【题目】给出一组式子:32+42=52,52+122=132,72+242=252,92+402=412,…
(1)你能发现关于上述式子的一些规律吗?
(2)请你运用规律,或者通过试验的方法(利用计算器),给出第五个式子.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区2014年10月的商品房均价约为15000元/平方米,将15000用科学记数法表示为( )
A. 1.5×104B. 1.5×105C. 0.15×104D. 0.15×105
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有下列结论:(1)三点确定一个圆;(2)弧的度数指弧所对圆周角的度数;(3)三角形的内心是三边中垂线交点,它到三角形各边的距离相等;(4)同圆或等圆中,弦相等则弦所对的弧相等。其中正确的个数有( )
A. 0B. 1C. 3D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某蓄水池的横断面示意图如右图,分深水区和浅水区,如果这个注满水的蓄水池以固定的流量把水全部放出.下面的图象能大致表示水的深度 ![]() 和放水时间
和放水时间 ![]() 之间的关系的是( )
之间的关系的是( )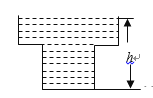
A.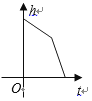
B.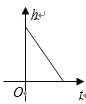
C.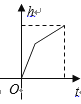
D.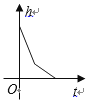
查看答案和解析>>
科目:初中数学 来源: 题型:
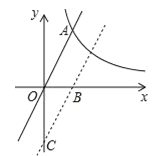
【题目】如图,已知抛物线与x轴交于A(-1,0),B(3,0),与y轴交于C(0,-3),顶点为点M.
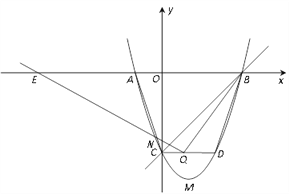
(1)求抛物线的解析式及点M的坐标.
(2)点P是直线BC在y轴右侧部分图象上的动点,若点P,点C,点M所构成的三角形与△AOC相似,求符合条件的P点坐标.
(3)过点C作CD∥AB,CD交抛物线于点D,点Q是线段CD上的一动点,作直线QN与线段AC交于点N,与x轴交于点E,且∠BQE=∠BDC,当CN的值最大时,求点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,抛物线y=x2-4x-5与x轴分别交于A、B(A在B的左边),与y轴交于点C,直线AP与y轴正半轴交于点M,交抛物线于点P,直线AQ与y轴负半轴交于点N,交抛物线于点Q,且OM=ON,过P、Q作直线l
(1) 探究与猜想:
① 取点M(0,1),直接写出直线l的解析式
取点M(0,2),直接写出直线l的解析式
② 猜想:
我们猜想直线l的解析式y=kx+b中,k总为定值,定值k为__________,请取M的纵坐标为n,验证你的猜想
(2) 如图2,连接BP、BQ.若△ABP的面积等于△ABQ的面积的3倍,试求出直线l的解析式

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com