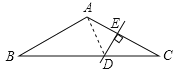
【题目】如图，在等腰△ABC中，∠BAC=120°，DE是AC的垂直平分线，DE=1cm，求BD的长．
【答案】4cm
【解析】试题分析：连接AD，先根据等腰三角形两底角相等求出∠B、∠C，根据线段垂直平分线上的点到两端点的距离相等可得AD=CD，根据等腰三角形两底角相等可得∠C=∠CAD，再求出∠BAD，然后根据直角三角形30°角所对的直角边等于斜边的一半求解即可．
试题解析：解：连接AD．∵等腰△ABC中，∠BAC=120°，∴∠B=∠C=
×（180°-120°）=30°．∵DE是AC的垂直平分线，∴AD=CD，∴∠C=∠CAD=30°，∴∠BAD=∠BAC-∠CAD=120°-30°=90°．∵DE=1cm，DE⊥AC，∴CD=2DE=2cm，∴AD=2cm．在Rt△ABD中，BD=2AD=2×2=4cm．
科目：初中数学 来源： 题型：
【题目】解决问题：
一辆货车从超市出发，向东走了3千米到达小彬家，继续走2.5千米到达小颖家，然后向西走了10千米到达小明家，最后回到超市．
（1）以超市为原点，以向东的方向为正方向，用1个单位长度表示1千米，在数轴上表示出小明家，小彬家，小颖家的位置．
（2）小明家距小彬家多远？
（3）货车一共行驶了多少千米？
（4）货车每千米耗油0.2升，这次共耗油多少升？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图是二次函数y=ax2+bx+c图象的一部分，过点（x1 ， 0），﹣3＜x1＜﹣2，对称轴为直线x=﹣1．给出四个结论：①abc＞0；②2a+b=0；③b2＞4ac；④3b+2c＞0，其中正确的结论有（ ） 
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，我市某中学课外活动小组的同学利用所学知识去测量釜溪河沙湾段的宽度．小宇同学在A处观测对岸C点，测得∠CAD=45°，小英同学在距A处50米远的B处测得∠CBD=30°，请你根据这些数据算出河宽．（精确到0.01米，参考数据 
≈1.414， 
≈1.732） 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知抛物线y=ax2+bx+c的顶点为D（﹣1，2），其部分图象如图所示，给出下列四个结论： ①a＜0； ②b2﹣4ac＞0；③2a﹣b=0；④若点P（x0 ， y0）在抛物线上，则ax02+bx0+c≤a﹣b+c．其中结论正确的是（ ）
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在边长为1的小正方形组成的网格中，△AOB的三个顶点均在格点上，点A、B的坐标分别为(3，2)、(1，3)．△AOB绕点O逆时针旋转90后得到△A1OB1．
（1）在网格中画出△A1OB1，并标上字母；
（2）点A关于O点中心对称的点的坐标为___________；
（3）点A1的坐标为________；
（4）△A1OB1的面积为_______________.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】地表以下岩层的温度T(℃)随着所处的深度h(km)的变化而变化，T与h之间在一定范围内近似地成一次函数关系．
(1)根据下表，求T(℃)与h(km)之间的函数关系式；
温度T(℃) | … | 90 | 160 | 300 | … |
深度h(km) | … | 2 | 4 | 8 | … |
(2)当岩层温度达到1770℃时，岩层所处的深度为多少？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
