
分析 将a看做已知数求出方程的解,表示出x,根据方程的解为自然数,确定出正数a的最大值与最小值,进而求解即可.
解答 解:去括号,得6x+3a-21+8=3x-2a+80,
移项合并得3x=93-5a,
解得:x=31-$\frac{5}{3}$a,
∵x为自然数,
∴31-$\frac{5}{3}$a≥0,且a为3的倍数,
解得a≤18$\frac{3}{5}$,且a为3的倍数,
∵a为正数,
∴a的最大值为18,最小值为3,
∴18+3=21.
即正数a的最大值与最小值的和是21.
点评 本题考查了一元一次方程的解的定义:使一元一次方程左右两边相等的未知数的值叫做一元一次方程的解.也考查了一元一次不等式.


科目:初中数学 来源: 题型:解答题
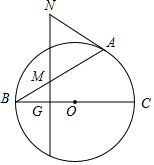 如图,BC是⊙O的弦,过⊙O上一点A作⊙O的切线AN,点M在AB上,过点M作BC的垂线交AN于点N,交直线BC于点G.
如图,BC是⊙O的弦,过⊙O上一点A作⊙O的切线AN,点M在AB上,过点M作BC的垂线交AN于点N,交直线BC于点G.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
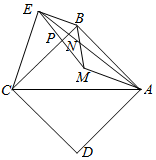 已知:如图,在正方形ABCD中,M为△ACB内一点,以AM为折痕将AC折叠过来得到线段AE,恰好使BE⊥CE,连接BM,AE与BM交于点N.
已知:如图,在正方形ABCD中,M为△ACB内一点,以AM为折痕将AC折叠过来得到线段AE,恰好使BE⊥CE,连接BM,AE与BM交于点N.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
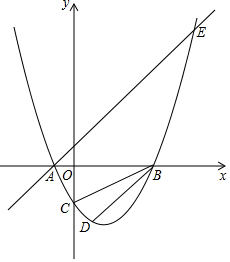 设抛物线y=ax2+bx-2与x轴交于两个不同的点A(-1,0)、B(m,0),与y轴交于点C,且∠ACB=90°.
设抛物线y=ax2+bx-2与x轴交于两个不同的点A(-1,0)、B(m,0),与y轴交于点C,且∠ACB=90°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com