
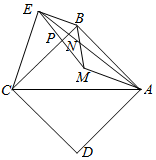
 已知:如图,在正方形ABCD中,M为△ACB内一点,以AM为折痕将AC折叠过来得到线段AE,恰好使BE⊥CE,连接BM,AE与BM交于点N.
已知:如图,在正方形ABCD中,M为△ACB内一点,以AM为折痕将AC折叠过来得到线段AE,恰好使BE⊥CE,连接BM,AE与BM交于点N.分析 (1)结论:AM⊥CE,由折叠的性质可知:AE=AC,∠EAM=∠CAM,所以△ACE是等腰三角形,利用三线合一即可证明.
(2)延长AM交CE于点G,则AG⊥CE,过点A作AH⊥EB交EB的延长线于点H.先证明四边形AHEG是矩形,再证明△AHB≌△BEC,推出EB=AH=EG=CG,由此即可解决问题.
(3)设AG与BC交于点K.由(2)可知,GK∥EB,GC=GE,推出CK=KB,设EB=a,则CE=2a,BC=AB=$\sqrt{5}$a,在Rt△ABK中,由∠ABK=90°,BK=$\frac{\sqrt{5}}{2}$a,AB=$\sqrt{5}$a,推出AK=$\sqrt{B{K}^{2}+A{B}^{2}}$=$\frac{5}{2}$a,由EB∥AK,推出$\frac{PB}{PK}$=$\frac{EB}{AK}$=$\frac{a}{\frac{5}{2}a}$=$\frac{2}{5}$,设PB=2k,PK=5k,则PC=CK+PK=7k+5k=12k,由此即可解决问题.
解答 (1)解:结论:AM⊥CE,理由如下:
由折叠的性质可知:AE=AC,∠EAM=∠CAM.
∴△ACE是等腰三角形,AM平分∠CAE.
∴AM⊥CE.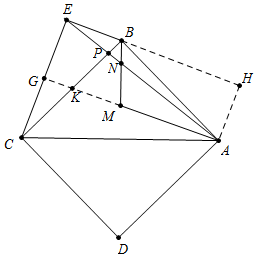
(2)证明:延长AM交CE于点G,则AG⊥CE 过点A作AH⊥EB交EB的延长线于点H.
∵AE=AC,
∴CG=EG.∵BE⊥CE,
∴∠AGE=∠GEH=∠H=90°,
∴四边形AGEH是矩形,
∴EG=AH.,
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,AC2=2BC2,
∵∠ABH+∠CBE=90°,∠CBE+∠BCE=90°,
∴∠ABH=∠BCE(同角的余角相等).
∵∠AHB=∠BEC=90°,
∴△AHB≌△BEC(AAS),
∴AH=BE.
∴EG=AH=BE=CG,
∴CE=2BE.
∵BC2=BE2+CE2=5BE2,AC2=2BC2.
∴AC2=10BE2.
(3)设AG与BC交于点K.
由(2)可知,GK∥EB,GC=GE,
∴CK=KB,设EB=a,则CE=2a,BC=AB=$\sqrt{5}$a,
在Rt△ABK中,∵∠ABK=90°,BK=$\frac{\sqrt{5}}{2}$a,AB=$\sqrt{5}$a,
∴AK=$\sqrt{B{K}^{2}+A{B}^{2}}$=$\frac{5}{2}$a,
∵EB∥AK,
∴$\frac{PB}{PK}$=$\frac{EB}{AK}$=$\frac{a}{\frac{5}{2}a}$=$\frac{2}{5}$,设PB=2k,PK=5k,则PC=CK+PK=7k+5k=12k,
∴$\frac{PB}{PC}$=$\frac{2k}{12k}$=$\frac{1}{6}$,
故答案为$\frac{1}{6}$.
点评 本题考查四边形综合题、正方形的性质、全等三角形的判定和性质、平行线等分线段定理,勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会利用参数解决问题,体现了数形结合的数学思想,属于中考压轴题.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 将边长为4的正方形ABCD向右倾斜,边长不变,∠ABC逐渐变小,顶点A、D及对角线BD的中点N分别运动到A′、D′和N′的位置,若∠A′BC=30°,则点N到点N′的运动路径长为$\frac{2π}{3}$.
将边长为4的正方形ABCD向右倾斜,边长不变,∠ABC逐渐变小,顶点A、D及对角线BD的中点N分别运动到A′、D′和N′的位置,若∠A′BC=30°,则点N到点N′的运动路径长为$\frac{2π}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
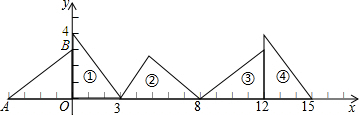
| A. | ①② | B. | ②③ | C. | ③ | D. | ④ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com