
| A. | 菱形是中心对称图形,但不是轴对称图形 | |
| B. | 相等的弦所对应的弦心距相等 | |
| C. | 直角三角形的外心和重心之间的距离等于斜边的六分之一 | |
| D. | 三角形的内心是三角形三边的中垂线的交点 |
分析 根据菱形的性质和对称的判定方法对A进行判断;根据圆心角、弧、弦、弦心距的关系对B进行判断;根据直角三角形的外心为斜边的中点和重心的性质对C进行判断;根据三角形内心的定义对D进行判断.
解答 解:A、菱形是中心对称图形,也是轴对称图形,所以A选项错误;
B、在同圆或等圆中,相等的弦所对应的弦心距相等,所以B选项错误;
C、直角三角形斜边上的中线等于斜边的一半,而重心到外心的距离等于斜边上的中线的$\frac{1}{3}$,所以直角三角形的外心和重心之间的距离等于斜边的六分之一,所以C选项正确;
D、三角形的内心是三角形三个角平分线的交点,所以D选项错误.
故选C.
点评 本题考查了命题与定理:判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果…那么…”形式. 2、有些命题的正确性是用推理证实的,这样的真命题叫做定理.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a2•a4=a8 | B. | (-2a2)3=-6a6 | C. | (x-2)2=x2-4 | D. | (-3)-2=$\frac{1}{9}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3.0591×103ug/m3 | B. | 3.0591×10-2ug/m3 | ||
| C. | 3.0591×102ug/m3 | D. | 3.0591×10-3ug/m3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
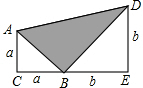 已知:两个等腰直角三角形(△ACB和△BED)边长分别为a和b(a<b)如图放置在一起,使得C、B、E在一条直线上,连接AD.求阴影部分(△ABD)的面积.
已知:两个等腰直角三角形(△ACB和△BED)边长分别为a和b(a<b)如图放置在一起,使得C、B、E在一条直线上,连接AD.求阴影部分(△ABD)的面积.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
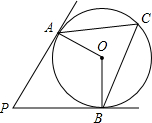 如图,PA,PB是圆O的两条切线,A,B分别是切点,点C是优弧AB上任意一点,连结OA,OB,CA,CB,∠P=60°,则∠ACB=60度.
如图,PA,PB是圆O的两条切线,A,B分别是切点,点C是优弧AB上任意一点,连结OA,OB,CA,CB,∠P=60°,则∠ACB=60度.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
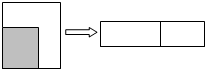 如图,边长为(m+2)的正方形纸片剪出一个边长为m的正方形之后余下部分又剪开拼成一个长方形(不重叠无缝隙),若拼成的长方形一边长为2,其面积是( )
如图,边长为(m+2)的正方形纸片剪出一个边长为m的正方形之后余下部分又剪开拼成一个长方形(不重叠无缝隙),若拼成的长方形一边长为2,其面积是( )| A. | 2m+4 | B. | 4m+4 | C. | m+4 | D. | 2m+2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com