
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
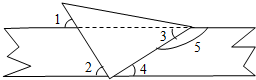
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
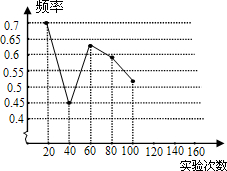 一粒木质中国象棋棋子“車”,它的正面雕刻一个“車”字,它的反面是平的,将棋子从一定高度下抛,落地反弹后可能是“車”字面朝上,也可能是“車”字朝下.由于棋子的两面不均匀,为了估计“車”字朝上的机会,某实验小组做了棋子下抛实验,并把实验数据整理如下:
一粒木质中国象棋棋子“車”,它的正面雕刻一个“車”字,它的反面是平的,将棋子从一定高度下抛,落地反弹后可能是“車”字面朝上,也可能是“車”字朝下.由于棋子的两面不均匀,为了估计“車”字朝上的机会,某实验小组做了棋子下抛实验,并把实验数据整理如下:| 实验次数 | 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 |
| “車”字朝上的频数 | 14 | 18 | 38 | 47 | 52 | 66 | 78 | 88 |
| 相应的频率 | 0.7 | 0.45 | 0.63 | 0.59 | 0.52 | 0.55 | 0.56 | 0.55 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 菱形是中心对称图形,但不是轴对称图形 | |
| B. | 相等的弦所对应的弦心距相等 | |
| C. | 直角三角形的外心和重心之间的距离等于斜边的六分之一 | |
| D. | 三角形的内心是三角形三边的中垂线的交点 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在四边形ABCD中,AB=DC,AD=BC,点E在BC上,点F在AD上,AF=CE,EF与对角线BD相交于点O,求证:EF与BD互相平分.
如图,在四边形ABCD中,AB=DC,AD=BC,点E在BC上,点F在AD上,AF=CE,EF与对角线BD相交于点O,求证:EF与BD互相平分.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
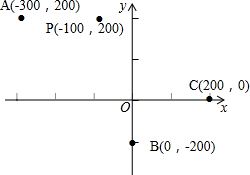 某地震多发地区有互相垂直的两条交通主干线,以这两条主干线为轴建立直角坐标系,1个单位长度为100km,地震监测部门测得该地区发生过一次地震,震中位置为P(-100,200),影响范围的半径为300km,如图所示,主干线沿线附近有3个城市:A(-300,200),B(0,-100),C(200,0),问在地震中受影响的是哪些城市?为什么?
某地震多发地区有互相垂直的两条交通主干线,以这两条主干线为轴建立直角坐标系,1个单位长度为100km,地震监测部门测得该地区发生过一次地震,震中位置为P(-100,200),影响范围的半径为300km,如图所示,主干线沿线附近有3个城市:A(-300,200),B(0,-100),C(200,0),问在地震中受影响的是哪些城市?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,AB是半圆的直径,点O为圆心,OA=5,弦AC=8,OD⊥AC,垂足为E,交⊙O于D,连接BE.设∠BEC=α,则tanα的值为( )
如图,AB是半圆的直径,点O为圆心,OA=5,弦AC=8,OD⊥AC,垂足为E,交⊙O于D,连接BE.设∠BEC=α,则tanα的值为( )| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{3\sqrt{13}}{13}$ | D. | $\frac{4\sqrt{13}}{13}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
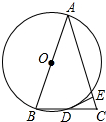 如图,△ABC中,AB=AC,以边AB为直径作⊙O,交BC于点D,过D作DE⊥AC于点E.
如图,△ABC中,AB=AC,以边AB为直径作⊙O,交BC于点D,过D作DE⊥AC于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com