
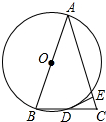
 如图,△ABC中,AB=AC,以边AB为直径作⊙O,交BC于点D,过D作DE⊥AC于点E.
如图,△ABC中,AB=AC,以边AB为直径作⊙O,交BC于点D,过D作DE⊥AC于点E.分析 (1)连接OD,AD,欲证DE是⊙O的切线,只需证明DE⊥OD即可;
(2)根据已知条件求得AD、BD'DC,利用△ABD∽△DCE对应边成比例求出CE的即可.
解答 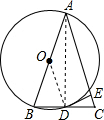 (1)证明:连接OD与AD,
(1)证明:连接OD与AD,
∵AB是⊙O的直径,
∴∠ADB=90°,
即AD⊥BC,
∵AB=AC,
∴BD=DC且∠B=∠C,
即D为BC的中点,
∵D为AB的中点,
∴OD∥AC,
∵DE⊥AC,
∴DE⊥OD,
∴DE为⊙O的切线.
(2)解:∵AB=13,sinB=$\frac{12}{13}$,
∴$\frac{AD}{AB}$=$\frac{12}{13}$,即AD=12,
∴BD=$\sqrt{A{B}^{2}-A{D}^{2}}$=$\sqrt{1{3}^{2}-1{2}^{2}}$=5,
∴DC=5,
在△ABD和△DCE中,∠B=∠C,∠CED=∠ABD=90°,
∴△ABD∽△DCE,
∴$\frac{DC}{AB}$=$\frac{CE}{BD}$,
∴CE=$\frac{BD•DC}{AB}$=$\frac{25}{13}$.
点评 本题主要考查了切线的判定以及相似三角形的判定和性质,解答本题的关键在于如何利用三角形相似求出CE的值.


科目:初中数学 来源: 题型:选择题
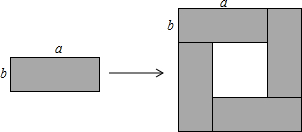 如图将4个长、宽分别均为a,b的长方形,摆成了一个大的正方形,利用面积的不同表示方法写出一个代数恒等式是( )
如图将4个长、宽分别均为a,b的长方形,摆成了一个大的正方形,利用面积的不同表示方法写出一个代数恒等式是( )| A. | a2+2ab+b2=(a+b)2 | B. | a2-2ab+b2=(a-b)2 | C. | 4ab=(a+b)2-(a-b)2 | D. | (a+b)(a-b)=a2-b2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
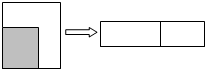 如图,边长为(m+2)的正方形纸片剪出一个边长为m的正方形之后余下部分又剪开拼成一个长方形(不重叠无缝隙),若拼成的长方形一边长为2,其面积是( )
如图,边长为(m+2)的正方形纸片剪出一个边长为m的正方形之后余下部分又剪开拼成一个长方形(不重叠无缝隙),若拼成的长方形一边长为2,其面积是( )| A. | 2m+4 | B. | 4m+4 | C. | m+4 | D. | 2m+2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点C是线段AB的中点.
如图,点C是线段AB的中点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
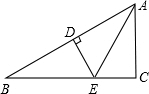 如图,AB的垂直平分线交AB于D,交BC于E,AE平分∠BAC,∠B=30°,DE=2cm,则BC的长是( )
如图,AB的垂直平分线交AB于D,交BC于E,AE平分∠BAC,∠B=30°,DE=2cm,则BC的长是( )| A. | 3cm | B. | 4cm | C. | 5cm | D. | 6cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com