
 如图,AB是半圆的直径,点O为圆心,OA=5,弦AC=8,OD⊥AC,垂足为E,交⊙O于D,连接BE.设∠BEC=α,则tanα的值为( )
如图,AB是半圆的直径,点O为圆心,OA=5,弦AC=8,OD⊥AC,垂足为E,交⊙O于D,连接BE.设∠BEC=α,则tanα的值为( )| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{3\sqrt{13}}{13}$ | D. | $\frac{4\sqrt{13}}{13}$ |
分析 连结BC,根据圆周角定理由AB是半圆的直径得∠ACB=90°,在Rt△ABC中,根据勾股定理计算出BC=6,再根据垂径定理由OD⊥AC得到AE=CE=$\frac{1}{2}$AC=4,再根据锐角三角函数的定义即可得出结论.
解答 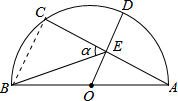 解:连结BC,如图,
解:连结BC,如图,
∵AB是半圆的直径,
∴∠ACB=90°,
在Rt△ABC中,AC=8,AB=10,
∴BC=$\sqrt{{AB}^{2}-{AC}^{2}}$=6,
∵OD⊥AC,
∴AE=CE=$\frac{1}{2}$AC=4,
∴tanα=$\frac{BC}{CE}$=$\frac{6}{4}$=$\frac{3}{2}$.
故选A.
点评 本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.


科目:初中数学 来源: 题型:选择题
 如图是小明在使用央视记者柴静关于雾霾调查纪录片《穹顶之下》中推荐的APP时的一张截图.它显示的是杭州10个地区的空气质量情况,你觉得用以下哪个统计量来表示整个杭州市的空气质量情况较合适.( )
如图是小明在使用央视记者柴静关于雾霾调查纪录片《穹顶之下》中推荐的APP时的一张截图.它显示的是杭州10个地区的空气质量情况,你觉得用以下哪个统计量来表示整个杭州市的空气质量情况较合适.( )| A. | 众数 | B. | 平均数 | C. | 中位数 | D. | 以上都可以 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
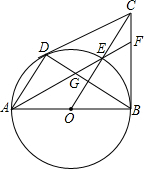 如图,已知AB为⊙O的直径,CD、CB为⊙O的切线,D、B为切点,OC交⊙O于点E,AE的延长线交BC于点F,连接AD、BD.给出以下结论:①AD∥OC;②FC=FE;③点E为△CDB的内心.其中正确的是①③(填序号).
如图,已知AB为⊙O的直径,CD、CB为⊙O的切线,D、B为切点,OC交⊙O于点E,AE的延长线交BC于点F,连接AD、BD.给出以下结论:①AD∥OC;②FC=FE;③点E为△CDB的内心.其中正确的是①③(填序号).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
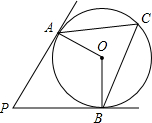 如图,PA,PB是圆O的两条切线,A,B分别是切点,点C是优弧AB上任意一点,连结OA,OB,CA,CB,∠P=60°,则∠ACB=60度.
如图,PA,PB是圆O的两条切线,A,B分别是切点,点C是优弧AB上任意一点,连结OA,OB,CA,CB,∠P=60°,则∠ACB=60度.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
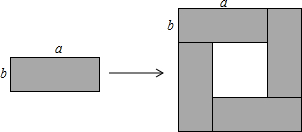 如图将4个长、宽分别均为a,b的长方形,摆成了一个大的正方形,利用面积的不同表示方法写出一个代数恒等式是( )
如图将4个长、宽分别均为a,b的长方形,摆成了一个大的正方形,利用面积的不同表示方法写出一个代数恒等式是( )| A. | a2+2ab+b2=(a+b)2 | B. | a2-2ab+b2=(a-b)2 | C. | 4ab=(a+b)2-(a-b)2 | D. | (a+b)(a-b)=a2-b2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com