
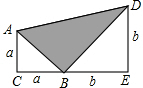
 已知:两个等腰直角三角形(△ACB和△BED)边长分别为a和b(a<b)如图放置在一起,使得C、B、E在一条直线上,连接AD.求阴影部分(△ABD)的面积.
已知:两个等腰直角三角形(△ACB和△BED)边长分别为a和b(a<b)如图放置在一起,使得C、B、E在一条直线上,连接AD.求阴影部分(△ABD)的面积. 分析 如图,直接求阴影部分的面积比较困难;因此,将所要求的三角形的面积转化为:求梯形ACED的面积-△ABC的面积-△BDE的面积,即可解决问题.
解答  解:阴影部分(△ABD)的面积
解:阴影部分(△ABD)的面积
=梯形ACED的面积-三角形ABC的面积-三角形BDE的面积
=$\frac{1}{2}$×(a+b)×(a+b)-$\frac{1}{2}$×a×a-$\frac{1}{2}$×b×b
=$\frac{1}{2}$(a2+b2+2ab)-$\frac{1}{2}{a}^{2}$-$\frac{1}{2}{b}^{2}$
=$\frac{1}{2}{a}^{2}+\frac{1}{2}{b}^{2}+ab-\frac{1}{2}{a}^{2}-\frac{1}{2}{b}^{2}$
=ab.
点评 该题主要考查了梯形的面积公式、三角形的面积公式及其应用问题;解题的关键是将所要求的三角形面积转化为梯形面积与另外两个三角形的面积之差.对运算求解能力也提出了一定的要求.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:填空题
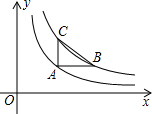 如图,已知点A在反比例函数y=$\frac{2}{x}$的图象上,点B,C分别在反比例函数y=$\frac{4}{x}$的图象上,且AB∥x轴,AC∥y轴,若AB=2AC,则点A的坐标为(2,1).
如图,已知点A在反比例函数y=$\frac{2}{x}$的图象上,点B,C分别在反比例函数y=$\frac{4}{x}$的图象上,且AB∥x轴,AC∥y轴,若AB=2AC,则点A的坐标为(2,1).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 菱形是中心对称图形,但不是轴对称图形 | |
| B. | 相等的弦所对应的弦心距相等 | |
| C. | 直角三角形的外心和重心之间的距离等于斜边的六分之一 | |
| D. | 三角形的内心是三角形三边的中垂线的交点 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
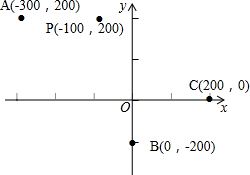 某地震多发地区有互相垂直的两条交通主干线,以这两条主干线为轴建立直角坐标系,1个单位长度为100km,地震监测部门测得该地区发生过一次地震,震中位置为P(-100,200),影响范围的半径为300km,如图所示,主干线沿线附近有3个城市:A(-300,200),B(0,-100),C(200,0),问在地震中受影响的是哪些城市?为什么?
某地震多发地区有互相垂直的两条交通主干线,以这两条主干线为轴建立直角坐标系,1个单位长度为100km,地震监测部门测得该地区发生过一次地震,震中位置为P(-100,200),影响范围的半径为300km,如图所示,主干线沿线附近有3个城市:A(-300,200),B(0,-100),C(200,0),问在地震中受影响的是哪些城市?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 平分弦的直径垂直于弦 | B. | 半圆(或直径)所对的圆周角是直角 | ||
| C. | 相等的圆心角所对的弧相等 | D. | 垂直半径的一端的直线是圆的切线 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com