
【题目】在平面直角坐标系xOy中,点A的坐标为(2,1),正比例函数y=kx的图象与线段OA的夹角是45°,求这个正比例函数的表达式为___________.
【答案】![]() 或
或![]()
【解析】由直线y=kx与线段OA的夹角是45°可知,本题有两种情况:一种是直线y=kx在线段OA的上方(即直线y=kx的图象经过第一、三象限);另一种是直线y=kx在线段OA的下方(直线y=kx的图象经过第二、四象限).再通过以直线y=kx与OA构造等腰直角三角形即可进行求解.
解:有两种情况:
①当直线y=kx在线段OA的上方时(即直线y=kx的图象经过第一、三象限),
如图所示,过点A作AB⊥OA,交直线y=kx于点B,过点A作平行于y轴的直线交x轴于点C,过点B作BD⊥AC,垂足为D.
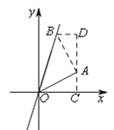
∵AB⊥OA
∴∠OAB=90°
∵∠BOA=45°
∴△OAB等腰直角三角形
∴OA=OB
∵∠OAC+∠BAD =90°, ∠OAC+∠AOC =90°
∴∠BAD=∠AOC
又∵∠D=∠ACO =90°
∴△OCA≌△BAD
∴AD=OC,BD=AC
∵A(2,1),
∴OC=2,AC=1
∴AD=OC=2,BD=AC=1
∴D点坐标为(2,3) ∴B点坐标为(1,3)
∴此时正比例函数表达式为:y=3x
②当直线y=kx在线段OA的下方时(即直线y=kx的图象经过第二、四象限):
过点A作AB⊥OA,交直线y=kx于点B,过点A作平行于x轴的直线交y轴于点C,过点B作BD⊥AC .

则由①可知:
∴△OCA≌△BAD
∴AD=OC,BD=AC
∵A(2,1),
∴OC=1,AC=2
∴AD=OC=1,BD=AC=2
∴D点坐标为(3,1)
∴B点坐标为(3,﹣1)
∴此时正比例函数表达式为:y=![]() x
x
∴正比例函数表达式为:![]() 或
或![]()


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:
【题目】某商场在“五一”期间举行促销活动,根据顾客按商品标价一次性购物总额,规定相应的优惠方法:①如果不超过500元,则不予优惠;②如果超过500元,但不超过800元,则按购物总额给予8折优惠;③如果超过800元,则其中800元给予8折优惠,超过800元的部分给予6折优惠.促销期间,小红和她母亲分别看中一件商品,若各自单独付款,则应分别付款480元和520元;若合并付款,则她们总共只需付款元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知不等式组 ![]() 的整数解为1、2、3,如果把适合这个不等式组的整数a、b组成有序数对(a,b),那么对应在平面直角坐标系上的点共有的个数为 .
的整数解为1、2、3,如果把适合这个不等式组的整数a、b组成有序数对(a,b),那么对应在平面直角坐标系上的点共有的个数为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(1,2),B(3,1),C(4,3).
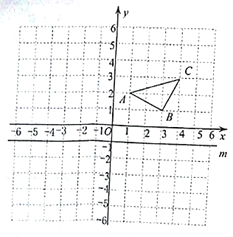
(1)作△ABC关于y轴的对称图形△A1B1C1,写出点C关于y轴的对称点C1的坐标;
(2)作△ABC关于直线m(直线m上各点的纵坐标都为-1)的对称图形△A2B2C2,写出点C关于直线m的对称点C2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB边的垂直平分线l交BC于点D,AC边的垂直平分线l2交BC于点E,l与 l2相交于点O,连接AD,AE,△ADE的为6cm.
(1)求BC的长;
(2)分别连接OA,OB,OC,若△OBC的周长为16cm,求OA的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,在⊙O中,AB,CD是直径,BE是切线,B为切点,
连接AD,BC,BD.
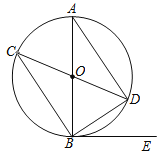
(1)求证:△ABD≌△CDB;
(2)若∠DBE=35°,求∠ADC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l1∥l2 , 点A是l1上的动点,点B在l1上,点C、D在l2上,∠ABC,∠ADC的平分线交于点E(不与点B,D重合).
(1)若点A在点B的左侧,∠ABC=80°,∠ADC=60°,过点E作EF∥l1 , 如图①所示,求∠BED的度数. 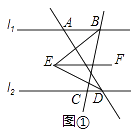
(2)若点A在点B的左侧,∠ABC=α°,∠ADC=60°,如图②所示,求∠BED的度数;(直接写出计算的结果) 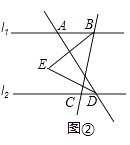
(3)若点A在点B的右侧,∠ABC=α°,∠ADC=60°,如图③所示,求∠BED的度数. 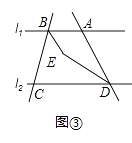
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
为了提高产品的附加值,某公司计划将研发生产的1200件新产品进行精加工后再投放市场.现有甲、乙两个工厂都具备加工能力,公司派出相关人员分别到这两个工厂了解情况,获得如下信息:
信息一:甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天;
信息二:乙工厂每天加工的数量是甲工厂每天加工数量的1.5倍.
根据以上信息,求甲、乙两个工厂每天分别能加工多少件新产品.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com