
分析 设这位同学骑摩托车的速度x千米每小时,则骑自行车的速度为$\frac{2}{5}$x千米每小时,由骑摩托车比骑自行车提前1小时到达,可由时间关系得到关于x的方程,解之即可得到这位同学骑摩托车的速度.
解答 解:设这位同学骑摩托车的速度x千米每小时,则骑自行车的速度为$\frac{2}{5}$x千米每小时,
∵骑摩托车比骑自行车提前1小时到达,
∴由时间关系可得关系式:$\frac{30}{x}$+1=$\frac{30}{\frac{2}{5}x}$,
解得x=45
根据经验可得x=45为方程的根.
答:这位同学骑摩托车的速度为45千米每小时.
点评 本题主要考查了分式方程在行程问题中的运用,找到等量关系:骑摩托车的速度是骑自行车速度的2.5倍才能按要求提前1小时到达,据此列出等式解得速度.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:解答题
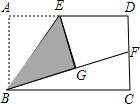 (1)操作发现:如图,小明在矩形纸片ABCD的边AD上取中点E,将△ABE沿BE折叠后得到△GBE,且点G在矩形ABCD内部,将BG延长交DC于点F,认为GF=DF,你同意吗?说明理由.
(1)操作发现:如图,小明在矩形纸片ABCD的边AD上取中点E,将△ABE沿BE折叠后得到△GBE,且点G在矩形ABCD内部,将BG延长交DC于点F,认为GF=DF,你同意吗?说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
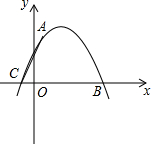 如图,二次函数y=ax2+bx+c的图象经过点A(1,4)与B(5,0),C(-1,0).
如图,二次函数y=ax2+bx+c的图象经过点A(1,4)与B(5,0),C(-1,0).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
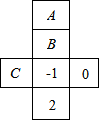 如图是一个正方体盒子的展开图,在其中三个正方形A、B、C内分别添入适当的数,使他们折成正方体后相对的面上的两个数互为相反数,则添入正方形A、B、C内的三个数中最小的是B面.
如图是一个正方体盒子的展开图,在其中三个正方形A、B、C内分别添入适当的数,使他们折成正方体后相对的面上的两个数互为相反数,则添入正方形A、B、C内的三个数中最小的是B面.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com