
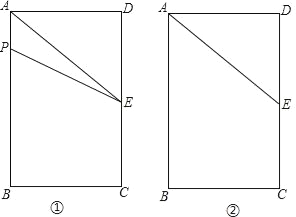
【题目】如图①,长方形ABCD中,AB=6cm,BC=4cm,E为CD的中点.点P从A点出发,沿A﹣B﹣C的方向在长方形边上匀速运动,速度为1cm/s,运动到C点停止.设点P运动的时间为ts.(图②为备用图)
(1)当P在AB上,t= s时,△APE的面积为长方形面积的![]() ;
;
(2)整个运动过程中,t为何值时,△APE为直角三角形?
【答案】(1)4;(2)当t=3s或t=![]() s时,△APE为直角三角形.
s时,△APE为直角三角形.
【解析】
(1)设t秒后,△APE的面积为长方形面积的![]() ,根据题意得:△APE的面积=
,根据题意得:△APE的面积=![]() APAD=
APAD=![]() t×4=
t×4=![]() ,从而求得t值;
,从而求得t值;
(2)①当P运动到AB中点时△AEP为直角三角形,此时∠APE为直角,t=3;②当P运动到BC上时,∠AEP为直角时利用相似三角形求得PB的长即可求得t值.
(1)设t秒后,△APE的面积为长方形面积的![]() ,根据题意得:AP=t,∴△APE的面积=
,根据题意得:AP=t,∴△APE的面积=![]() APAD=
APAD=![]() t×4=
t×4=![]() ,解得:t=4,∴4秒后,△APE的面积为长方形面积的
,解得:t=4,∴4秒后,△APE的面积为长方形面积的![]() ;
;
(2)①当t=3时,AP=3,如图1所示:
∵E为CD的中点,∴CE=DE=3.
∵四边形ABCD是矩形,BC=AD=4,∴四边形APED是矩形,∴PE⊥AB,∴△APE是直角三角形;
②当P在BC上时,若△APE是直角三角形,∠AED+∠PEC=90°,如图2所示:
∵∠ADE=∠ECP=90°,∴∠AED=∠EPC,∴△ADE∽△ECP,∴![]() =
=![]() ,解得:CP=
,解得:CP=![]() =
=![]() =
=![]() ,∴PB=BC﹣PC=4﹣
,∴PB=BC﹣PC=4﹣![]() =
=![]() ,∴t=6+
,∴t=6+![]() =
=![]() .
.
综上所述:当t=3s或t=![]() s时,△APE为直角三角形.
s时,△APE为直角三角形.


科目:初中数学 来源: 题型:
【题目】如图,已知∠ABC=∠DCB,添加一个条件使△ABC≌△DCB,下列添加的条件不能使△ABC≌△DCB的是( )

A. ∠A=∠D B. AB=DC C. AC=DB D. OB=OC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“十一”长假期间,小张和小李决定骑自行车外出旅游,两人相约一早从各自家中出发,已知两家相距10千米,小张出发必过小李家.
(1)若两人同时出发,小张车速为20千米,小李车速为15千米,经过多少小时能相遇?
(2)若小李的车速为10千米,小张提前20分钟出发,两人商定小李出发后半小时二人相遇,则小张的车速应为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,将长方形纸片的一角作折叠,使顶点A落在A′处,EF为折痕,若EA′恰好平分∠FEB,求∠FEB的度数.

(2)如图,A地和B地都是海上观测站,从A地发现它的北偏东60方向有一艘船P,同时,从B地发现这艘船P在它北偏东30方向.试在图中画出这艘船P的位置.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题7分)如图,在Rt△ABC中,∠ACB=90°,E为AC上一点,且AE=BC,过点A作AD⊥CA,垂足为A,且AD=AC,AB、DE交于点F.
(1)判断线段AB与DE的数量关系和位置关系,并说明理由;
(2)连接BD、BE,若设BC=a,AC=b,AB=c,请利用四边形ADBE的面积证明勾股定理.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在升旗结束后,小铭想利用所学数学知识测量学校旗杆高度,如图,旗杆的顶端垂下一绳子,将绳子拉直钉在地上,末端恰好至C处且与地面成60°角,小铭从绳子末端C处拿起绳子后退至E点,求旗杆AB的高度和小铭后退的距离.(单位:米,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,结果保留一位小数)
≈1.73,结果保留一位小数)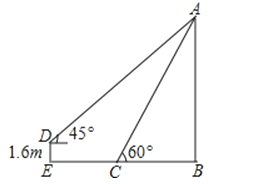
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,扇形AOB中,半径OA=2,∠AOB=120°,C是 ![]() 的中点,连接AC、BC,则图中阴影部分面积是( )
的中点,连接AC、BC,则图中阴影部分面积是( ) 
A.![]() ﹣2
﹣2 ![]()
B.![]() ﹣2
﹣2 ![]()
C.![]() ﹣
﹣ ![]()
D.![]() ﹣
﹣ ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴是一个非常重要的数学工具,通过它把数和数轴上的点建立起对应关系,揭示了数与点之间的内在联系,它是“数形结合”的基础.已知数轴上有点A和点B,点A和点B分别表示数-20和40,请解决以下问题:
(1)请画出数轴,并标明A、B两点;
(2)若点P、Q分别从点A、点B同时出发,相向而行,点P、Q移动的速度分别为每秒4个单位长度和2个单位长度.问:当P、Q相遇于点C时,C所对应的数是多少?
(3)若点P、Q分别从点A、点B同时出发,沿x轴正方向同向而行,点P、Q移动的速度分别为每秒4个单位长度和2个单位长度.问:当P、Q相遇于点D时,D所对应的数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
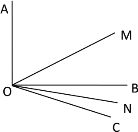
【题目】如图,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC.
(1)求∠MON的度数;
(2)若题干中的∠AOB=![]() ,其他条件不变,求∠MON的度数;
,其他条件不变,求∠MON的度数;
(3)若题干中的∠BOC=![]() (
(![]() 为锐角),其他条件不变,求∠MON的度数;
为锐角),其他条件不变,求∠MON的度数;
(4)综合(1)(2)(3)的结果,你能得出什么结论?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com