
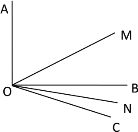
【题目】如图,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC.
(1)求∠MON的度数;
(2)若题干中的∠AOB=![]() ,其他条件不变,求∠MON的度数;
,其他条件不变,求∠MON的度数;
(3)若题干中的∠BOC=![]() (
(![]() 为锐角),其他条件不变,求∠MON的度数;
为锐角),其他条件不变,求∠MON的度数;
(4)综合(1)(2)(3)的结果,你能得出什么结论?
【答案】(1)∠MON=45°;(2)∠MON=![]()
![]() ;(3)∠MON=45°;(4)∠MON的大小始终等于∠AOB的一半,与∠BOC的大小没有关系.
;(3)∠MON=45°;(4)∠MON的大小始终等于∠AOB的一半,与∠BOC的大小没有关系.
【解析】
(1)根据题意,易得∠MOC![]() ∠AOC,∠NOC
∠AOC,∠NOC![]() ∠BOC进而结合∠MON=∠MOC﹣∠NOC的关系,易得答案;
∠BOC进而结合∠MON=∠MOC﹣∠NOC的关系,易得答案;
(2)由(1)的结论,易得当∠AOB=α°时,总有∠MON![]() ∠AOB的关系,即得答案;
∠AOB的关系,即得答案;
(3)由(1)的结论,易得当∠BOC=β°(∠BOC为锐角)时,总有∠MON![]() ∠AOB的关系,即得答案;
∠AOB的关系,即得答案;
(4)分析(1)(2)(3)的结论,易得答案.
(1)∵OM平分∠AOC,ON平分∠BOC,∴∠MOC![]() ∠AOC,∠NOC
∠AOC,∠NOC![]() ∠BOC.
∠BOC.
又∵∠AOB=90°,∠BOC=30°,∴∠MON=∠MOC﹣∠NOC![]() ∠AOC
∠AOC![]() ∠BOC
∠BOC![]() (∠AOC﹣∠BOC)
(∠AOC﹣∠BOC)![]() ∠AOB=
∠AOB=![]() ×90°=45°.
×90°=45°.
(2)当∠AOB=α,其他条件不变时,∠MON![]() ∠AOB
∠AOB![]() α.
α.
(3)当∠BOC=β,其他条件不变时,∠MON![]() ∠AOB
∠AOB![]() 90°=45°.
90°=45°.
(4)由(1)(2)(3)的结果,可得出结论:∠MON总等于∠AOB的一半,而与∠BOC的大小无关.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:
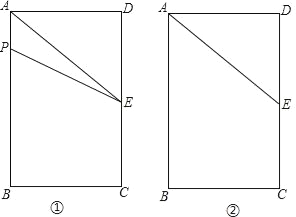
【题目】如图①,长方形ABCD中,AB=6cm,BC=4cm,E为CD的中点.点P从A点出发,沿A﹣B﹣C的方向在长方形边上匀速运动,速度为1cm/s,运动到C点停止.设点P运动的时间为ts.(图②为备用图)
(1)当P在AB上,t= s时,△APE的面积为长方形面积的![]() ;
;
(2)整个运动过程中,t为何值时,△APE为直角三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,O为直线AB上一点,过点O作射线OC,∠AOC=30°,将一直角三角尺(∠M=30°)的直角顶点放在点O处,一边ON在射线OA上,另一边OM与OC都在直线AB的上方.
(1)若将图1中的三角尺绕点O以每秒5°的速度,沿顺时针方向旋转t秒,当OM恰好平分∠BOC时,如图2.
①求t值;
②试说明此时ON平分∠AOC;
(2)将图1中的三角尺绕点O顺时针旋转,设∠AON=α,∠COM=β,当ON在∠AOC内部时,试求α与β的数量关系;
(3)若将图1中的三角尺绕点O以每秒5°的速度沿顺时针方向旋转的同时,射线OC也绕点O以每秒8°的速度沿顺时针方向旋转,如图3,那么经过多长时间,射线OC第一次平分∠MON?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
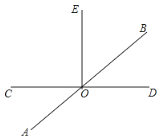
【题目】如图,已知直线AB和CD相交于点O,在∠COB的内部作射线OE.
(1)若∠AOC=36°,∠COE=90°,求∠BOE的度数;
(2)若∠COE:∠EOB:∠BOD=4:3:2,求∠AOE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)自2014年12月启动“绿茵行动,青春聚力”郴州共青林植树活动以来,某单位筹集7000元购买了桂花树和樱花树共30棵,其中购买桂花树花费3000元.已知桂花树比樱花树的单价高50%,求樱花树的单价及棵树.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题:①对顶角相等;②同位角相等,两直线平行;③若|a|=|b|,则a=b;④若x=2,则2|x|-1=3.以上命题是真命题的有( ).
A. ①②③④ B. ①④ C. ②④ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节前夕,小东的父母准备购买若干个粽子和咸鸭蛋(每个粽子的价格相同,每个咸鸭蛋的价格相同).已知粽子的价格比咸鸭蛋的价格贵1.8元,花30元购买粽子的个数与花12元购买咸鸭蛋的个数相同,求粽子与咸鸭蛋的价格各多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
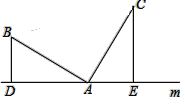
【题目】问题发现:如图,已知:AB=AC,∠BAC=90°,直线m经过点A,过点B作BD⊥m于D, CE⊥m于E.我们把这种常见图形定义为“K”字图.很容易得到线段DE、BD、CE之间的数量关系是 .
拓展探究:如图2,若AB=AC,∠BAC=∠BDA=∠AEC,则线段DE、BD、CE之间的数量关系还成立吗?如果成立,请证明之.
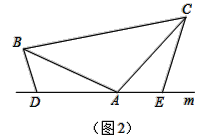
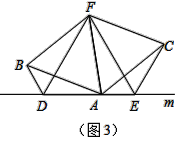
解决问题:如图3,若AB=AC,∠BAC=∠BDA=∠AEC=120°,点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,BD=2,CE=4,求△DEF的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,∠BAC=120,AD⊥BC,且AD=AB.
(1)如图1,DE⊥AB,DF⊥AC,垂足分别为点E,F,求证:AE+AF=AD
(2)如图2,如果∠EDF=60,且∠EDF两边分别交边AB,AC于点E,F,那么线段AE,AF,AD之间有怎样的数量关系?并给出证明.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com