
【题目】如图1,O为直线AB上一点,过点O作射线OC,∠AOC=30°,将一直角三角尺(∠M=30°)的直角顶点放在点O处,一边ON在射线OA上,另一边OM与OC都在直线AB的上方.
(1)若将图1中的三角尺绕点O以每秒5°的速度,沿顺时针方向旋转t秒,当OM恰好平分∠BOC时,如图2.
①求t值;
②试说明此时ON平分∠AOC;
(2)将图1中的三角尺绕点O顺时针旋转,设∠AON=α,∠COM=β,当ON在∠AOC内部时,试求α与β的数量关系;
(3)若将图1中的三角尺绕点O以每秒5°的速度沿顺时针方向旋转的同时,射线OC也绕点O以每秒8°的速度沿顺时针方向旋转,如图3,那么经过多长时间,射线OC第一次平分∠MON?请说明理由.

【答案】(1)①t=3;②见解析;(2)β=α+60°;(3)t=5时,射线OC第一次平分∠MON.
【解析】
(1)根据角平分线的性质以及余角补角的性质即可得出结论;
(2)根据∠NOC=∠AOC-∠AON=90°-∠MOC即可得到结论;
(3)分别根据转动速度关系和OC平分∠MON列方程求解即可.
(1)①∵∠AOC=30°,OM平分∠BOC,∴∠BOC=2∠COM=2∠BOM=150°,∴∠COM=∠BOM=75°.
∵∠MON=90°,∴∠CON=15°,∠AON+∠BOM=90°,∴∠AON=∠AOC﹣∠CON=30°﹣15°=15°,∴∠AON=∠CON,∴t=15°÷3°=5秒;
②∵∠CON=15°,∠AON=15°,∴ON平分∠AOC.
(2)∵∠AOC=30°,∴∠NOC=∠AOC-∠AON=90°-∠MOC,∴30°-α=90°-β,∴β=α+60°;
(3)设旋转时间为t秒,∠AON=5t,∠AOC=30°+8t,∠CON=45°,∴30°+8t=5t+45°,∴t=5.
即t=5时,射线OC第一次平分∠MON.


科目:初中数学 来源: 题型:
【题目】“十一”长假期间,小张和小李决定骑自行车外出旅游,两人相约一早从各自家中出发,已知两家相距10千米,小张出发必过小李家.
(1)若两人同时出发,小张车速为20千米,小李车速为15千米,经过多少小时能相遇?
(2)若小李的车速为10千米,小张提前20分钟出发,两人商定小李出发后半小时二人相遇,则小张的车速应为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,扇形AOB中,半径OA=2,∠AOB=120°,C是 ![]() 的中点,连接AC、BC,则图中阴影部分面积是( )
的中点,连接AC、BC,则图中阴影部分面积是( ) 
A.![]() ﹣2
﹣2 ![]()
B.![]() ﹣2
﹣2 ![]()
C.![]() ﹣
﹣ ![]()
D.![]() ﹣
﹣ ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴是一个非常重要的数学工具,通过它把数和数轴上的点建立起对应关系,揭示了数与点之间的内在联系,它是“数形结合”的基础.已知数轴上有点A和点B,点A和点B分别表示数-20和40,请解决以下问题:
(1)请画出数轴,并标明A、B两点;
(2)若点P、Q分别从点A、点B同时出发,相向而行,点P、Q移动的速度分别为每秒4个单位长度和2个单位长度.问:当P、Q相遇于点C时,C所对应的数是多少?
(3)若点P、Q分别从点A、点B同时出发,沿x轴正方向同向而行,点P、Q移动的速度分别为每秒4个单位长度和2个单位长度.问:当P、Q相遇于点D时,D所对应的数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为某校九年级男子立定跳远成绩的统计图,从左到右各分数段的人数之比为1∶2∶5∶6∶4,第四组的频数是12.有下面的4个结论:
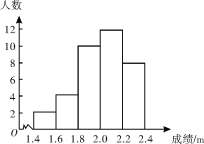
①一共测试了36名男生的成绩;②男子立定跳远成绩的中位数分布在1.8~2.0组;③男子立定跳远成绩的平均数不超过2.2;④如果男子立定跳远成绩低于1.85 m为不合格,那么不合格人数为6人.
其中结论正确的是( )
A. ①③ B. ①④ C. ②③ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上三点M,O,N对应的数分别为-3,0,1,点P为数轴上任意一点,其对应的数为x.
(1)如果点P到点M,点N的距离相等,那么x的值是______________;
(2)数轴上是否存在点P,使点P到点M,点N的距离之和是5?若存在,请直接写出x的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,AB=3,BC=8,点D为BC的中点,将△ABD沿AD折叠,使点B落在点E处,连接CE,则CE的长为_________.
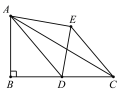
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC.
(1)求∠MON的度数;
(2)若题干中的∠AOB=![]() ,其他条件不变,求∠MON的度数;
,其他条件不变,求∠MON的度数;
(3)若题干中的∠BOC=![]() (
(![]() 为锐角),其他条件不变,求∠MON的度数;
为锐角),其他条件不变,求∠MON的度数;
(4)综合(1)(2)(3)的结果,你能得出什么结论?
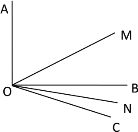
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知不在同一条直线上的三点A,B,C.
(1)按下列要求作图(用尺规作图,不要求写做法,但要保留作图痕迹,并书写结论)
①分别作射线BA,线段AC;
②在线段BA的延长线上作AD=AC.
(2)若∠CAD比∠CAB大100°,则∠CAB的度数为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com