
【题目】已知二次函数![]() ,完成下列各题:
,完成下列各题:

![]() 将函数关系式用配方法化为
将函数关系式用配方法化为![]() 的形式,并写出它的顶点坐标、对称轴.
的形式,并写出它的顶点坐标、对称轴.
![]() 求出它的图象与坐标轴的交点坐标.
求出它的图象与坐标轴的交点坐标.
![]() 在直角坐标系中,画出它的图象.
在直角坐标系中,画出它的图象.
![]() 根据图象说明:当
根据图象说明:当![]() 为何值时,
为何值时,![]() ;当
;当![]() 为何值时,
为何值时,![]() .
.
【答案】(1)![]() ,顶点(2,9),对称轴x=2
,顶点(2,9),对称轴x=2
(2)与x轴交点(5,0)(-1,0),与y轴交点(0,5)
(3)图略
(4)当-1<x<5时,y>0,当x>5或x<-1时,y<0。
【解析】
试题(1)用配方法整理,进而得出顶点坐标和对称轴即可;
(2)让函数值为0,求得一元二次方程的两个解即为这个二次函数的图象与坐标轴的交点的横坐标,让x=0,可求得抛物线与y轴的交点坐标;找到与y轴的交点,x轴的交点,对称轴,即可画出大致图象;
(3)由(1)和(2)中的条件即可画出它的图象;
(4)分别找到x轴上方和下方函数图象所对应的自变量的取值即可.
试题解析:(1)y=-x2+4x+5=-(x2-4x+4)+9=-(x-2)2+9;
故它的顶点坐标为(2,9)、对称轴为:x=2;(2)图象与x轴相交是y=0,则:
0=-(x-2)2+9,
解得x1=5,x2=-1,
∴这个二次函数的图象与x轴的交点坐标为(5,0),(-1,0);
当x=0时,y=5,
∴与y轴的交点坐标为(0,5);
(3)画出大致图象为
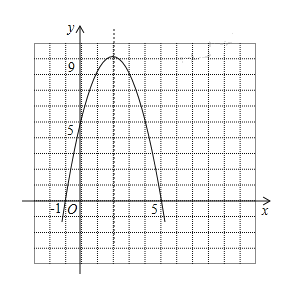 ;
;
4)-1<x<5时 y>0;x<-1或x>5时 y<0.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:
【题目】 为更新果树品种,某果园计划新购进A、B两个品种的果树苗栽植培育,若计划购进这两种果树苗共45棵,其中A种苗的单价为7元/棵,购买B种苗所需费用y(元)与购买数量x(棵)之间存在如图所示的函数关系.
(1)求y与x的函数关系式;
(2)若在购买计划中,B种苗的数量不超过35棵,但不少于A种苗的数量,请设计购买方案,使总费用最低,并求出最低费用.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把抛物线y=![]() x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=
x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=![]() x2交于点Q,则图中阴影部分的面积为 ▲ .
x2交于点Q,则图中阴影部分的面积为 ▲ .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市团委举办“我的中国梦”为主题的知识竞赛,甲、乙两所学校参赛人数相等,比赛结束后,发现学生成绩分别为70分、80分、90分、100分,并根据统计数据绘制了如下不完整的统计图表:

乙校成绩统计表
分数/分 | 人数/人 |
70 | 7 |
80 | |
90 | 1 |
100 | 8 |
(1)在图①中,“80分”所在扇形的圆心角度数为________;
(2)请你将图②补充完整;
(3)求乙校成绩的平均分;
(4)经计算知s甲2=135,s乙2=175,请你根据这两个数据,对甲、乙两校成绩作出合理评价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)图象如图所示,下列结论:①abc<0;②2a﹣b<0;③b2>(a+c)2;④点(﹣3,y1),(1,y2)都在抛物线上,则有y1>y2.其中正确的结论有( )
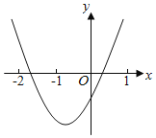
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的周长为19,点D,E在边BC上,∠ABC的平分线垂直于AE,垂足为N,∠ACB的平分线垂直于AD,垂足为M,若BC=7,则MN的长度为( )

A. ![]() B. 2 C.
B. 2 C. ![]() D. 3
D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一个长为4a、宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图2).

(1)图2中的阴影部分的面积为 ;
(2)观察图2请你写出(a+b)2、(a﹣b)2、ab之间的等量关系是 ;
(3)根据(2)中的结论,若x+y=7,xy=![]() ,则x﹣y= ;
,则x﹣y= ;
(4)实际上通过计算图形的面积可以探求相应的等式.根据图3,写出一个因式分解的等式 .
查看答案和解析>>
科目:初中数学 来源: 题型:
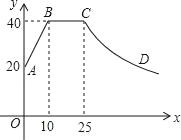
【题目】心理学家研究发现,一般情况下,一节课40分钟中,学生的注意力随教师讲课的变化而变化.开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数y随时间x(分钟)的变化规律如图所示(其中AB,BC分别为线段,CD为双曲线的一部分):
(1)分别求出线段AB和曲线CD的函数关系式;
(2)开始上课后第五分钟时与第三十分钟时相比较,何时学生的注意力更集中?
(3)一道数学竞赛题,需要讲19分钟,为了效果较好,要求学生的注意力指标数最低达到36,那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com