【题目】 为更新果树品种，某果园计划新购进A、B两个品种的果树苗栽植培育，若计划购进这两种果树苗共45棵，其中A种苗的单价为7元/棵，购买B种苗所需费用y（元）与购买数量x（棵）之间存在如图所示的函数关系．
（1）求y与x的函数关系式；
（2）若在购买计划中，B种苗的数量不超过35棵，但不少于A种苗的数量，请设计购买方案，使总费用最低，并求出最低费用．
【答案】（1）y=6.4x+32；（2）当购买数量x=35时，W总费用最低，W最低=137元．
【解析】
试题（1）利用得到系数法求解析式，列出方程组解答即可；（2）根据所需费用为W=A种树苗的费用+B种树苗的费用，即可解答．
试题解析：（1）设y与x的函数关系式为：y=kx+b， 把（20，160），（40，288）代入y=kx+b得：
解得：
∴y=6.4x+32．
（2）∵B种苗的数量不超过35棵，但不少于A种苗的数量，∴
∴22.5≤x≤35，
设总费用为W元，则W=6.4x+32+7（45﹣x）=﹣0.6x+347，
∵k=﹣0.6， ∴y随x的增大而减小， ∴当x=35时，W总费用最低，W最低=﹣0.6×35+347=137（元）．
名校课堂系列答案科目：初中数学 来源： 题型：
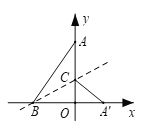
【题目】如图，在平面直角坐标系中，已知点A（0，12），B（－5，0），连接AB．将△AOB沿过点B的直线折叠，使点A落在x轴上的点
处，折痕所在的直线交y轴正半轴于点C，则点C的坐标为___________________________.
查看答案和解析>>
科目：初中数学 来源： 题型：
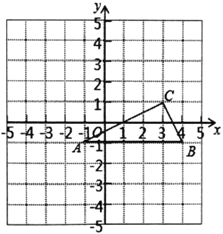
【题目】如图，
的三个顶点在边长为1的正方形网格中，已知
，
，
.
(1)画出关于
轴对称的
(其中
，
，
分别是
，
，
的对应点，不写画法)；
(2)分别写出，，三点的坐标.
(3)请写出所有以
为边且与全等的三角形的第三个顶点(不与重合)的坐标_____.
查看答案和解析>>
科目：初中数学 来源： 题型：
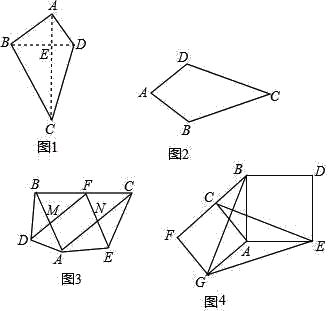
【题目】阅读理解：如图1，我们把对角线互相垂直的四边形叫做垂美四边形．垂美四边形有如下性质：
垂美四边形的两组对边的平方和相等．
已知：如图1，四边形ABCD是垂美四边形，对角线AC、BD相交于点E．
求证：AD2+BC2=AB2+CD2
证明：∵四边形ABCD是垂美四边形
∴AC⊥BD，
∴∠AED=∠AEB=∠BEC=∠CED=90°，
由勾股定理得，AD2+BC2=AE2+DE2+BE2+CE2，
AB2+CD2=AE2+BE2+CE2+DE2，
∴AD2+BC2=AB2+CD2．
拓展探究：
（1）如图2，在四边形ABCD中，AB=AD，CB=CD，问四边形ABCD是垂美四边形吗？请说明理由．
（2）如图3，在Rt△ABC中，点F为斜边BC的中点，分别以AB，AC为底边，在Rt△ABC外部作等腰三角形ABD和等腰三角形ACE，连接FD，FE，分别交AB，AC于点M，N．试猜想四边形FMAN的形状，并说明理由；
问题解决：
如图4，分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE，连接CE，BG，GE，已知AC=4，AB=5．求GE长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知如图等腰
，
，
，
于点D，点P是BA延长线上一点，点O是线段AD上一点，
，下面的结论：
；
是等边三角形；
；
其中正确的是
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（8分）如图，在△ABC中，∠C=60°，∠A=40°．
（1）用尺规作图作AB的垂直平分线，交AC于点D，交AB于点E（保留作图痕迹，不要求写作法和证明）；
（2）求证：BD平分∠CBA．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列说法：
①无理数都是无限小数；
②
的算术平方根是3；
③数轴上的点与实数一一对应；
④平方根与立方根等于它本身的数是0和1；
⑤若点A（-2，3）与点B关于x轴对称，则点B的坐标是（-2，-3）.
其中正确的个数是( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
