
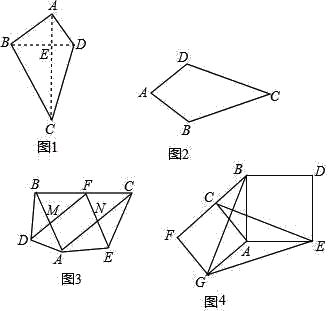
【题目】阅读理解:如图1,我们把对角线互相垂直的四边形叫做垂美四边形.垂美四边形有如下性质:
垂美四边形的两组对边的平方和相等.
已知:如图1,四边形ABCD是垂美四边形,对角线AC、BD相交于点E.
求证:AD2+BC2=AB2+CD2
证明:∵四边形ABCD是垂美四边形
∴AC⊥BD,
∴∠AED=∠AEB=∠BEC=∠CED=90°,
由勾股定理得,AD2+BC2=AE2+DE2+BE2+CE2,
AB2+CD2=AE2+BE2+CE2+DE2,
∴AD2+BC2=AB2+CD2.
拓展探究:
(1)如图2,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂美四边形吗?请说明理由.
(2)如图3,在Rt△ABC中,点F为斜边BC的中点,分别以AB,AC为底边,在Rt△ABC外部作等腰三角形ABD和等腰三角形ACE,连接FD,FE,分别交AB,AC于点M,N.试猜想四边形FMAN的形状,并说明理由;
问题解决:
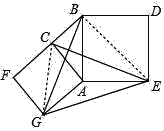
如图4,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连接CE,BG,GE,已知AC=4,AB=5.求GE长.
【答案】拓展探究:(1)四边形ABCD是垂美四边形,理由详见解析;(2)四边形FMAN是矩形,理由详见解析;问题解决:![]() .
.
【解析】
(1)根据垂直平分线的判定定理可得直线AC是线段BD的垂直平分线,进而得证;
(2)首先猜想出结论,根据垂直的定义可得∠AOD=∠AOB=∠BOC=∠COD=90°,由勾股定理得AD2+BC2=AO2+DO2+BO2+CO2,进而证得猜想,将已知代入即可求得CD;
(3)根据垂美四边形的性质、勾股定理、结合(2)的结论计算即可.
拓展探究:(1)四边形ABCD是垂美四边形,
理由如下:
∵AB=AD,
∴点A在线段BD的垂直平分线上,
∵CB=CD,
∴点C在线段BD的垂直平分线上,
∴直线AC是线段BD的垂直平分线,
∴AC⊥BD,即四边形ABCD是垂美四边形.
(2)四边形FMAN是矩形,
理由:如图3,连接AF,
∵Rt△ABC中,点F为斜边BC的中点,
∴AF=CF=BF,
又∵等腰三角形ABD和等腰三角形ACE,
∴AD=DB、AE=CE,
∴由(1)可得,DF⊥AB,EF⊥AC,
又∵∠BAC=90°,
∴∠AMF=∠MAN=∠ANF=90°,
∴四边形AMFN是矩形;
问题解决:
连接CG、BE,
∵∠CAG=∠BAE=90°,
∴∠CAG+∠BAC=∠BAE+∠BAC,即∠GAB=∠CAE,
∵在△GAB和△CAE中,AG=AC,∠GAB=∠CAE,AB=AE,
∴△GAB≌△CAE,
∴∠ABG=∠AEC,
又∠AEC+∠AME=90°,
∴∠ABG+∠AME=90°,即CE⊥BG,
∴四边形CGEB是垂美四边形,
∴CG2+BE2=CB2+GE2,
∵AC=4,AB=5,
∴BC=3,CG=![]() ,BE=
,BE=![]() ,
,
∴GE2=CG2+BE2﹣CB2=73,
∴GE=![]()


科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2+(k+3)x+![]() =0有两个不相等的实数根.
=0有两个不相等的实数根.
(1)求k的取值范围;
(2)若方程两根为x1,x2,那么是否存在实数k,使得等式![]() =﹣1成立?若存在,求出k的值;若不存在,请说明理由.
=﹣1成立?若存在,求出k的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
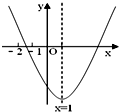
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,现有下列结论:①b2﹣4ac>0 ②a>0 ③b>0 ④c>0 ⑤9a+3b+c<0,则其中结论正确的个数是( )
A、2个B、3个
C、4个D、5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读探索
问题背景:著名数学家华罗庚提出把“数形关系”(勾股定理)带到其他星球,作为地球人与其他星球“人”进行第一次”谈话“的语言.2002年8月在北京召开的国际数学大会会标取材于我国古代数学家赵爽的《勾股圆方图注》,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形(如图1所示).勾股定理是一条古老的数学定理,它有很多种证明方法,我国汉代数学家赵爽根据弦图,利用面积进行了证明.
赵爽证明方法如下:
以a、b为直角边(b>a),以c为斜边作四个全等的直角三角形,则每个直角三角形的面积等于![]() ,把这四个直角三角形拼成如图1所示形状.
,把这四个直角三角形拼成如图1所示形状.
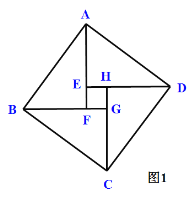
∵Rt△DAE≌Rt△ABF
∴∠EDA=∠FAB
∵∠EAD+∠EDA=90°
∴∠FAB+∠EAD=90°
∴四边形ABCD是一个边长为c的正方形,它的面积等于![]()
∵EF=FG=GH=HE=b-a
∠HEF=90°
∴四边形EFGH是一个边长为b-a的正方形,它的面积等于![]()
∴![]()
∴![]() 从而证明了勾股定理.
从而证明了勾股定理.
思维拓展:
1、如果大正方形的面积为13,小正方形的面积为1,直角三角形的较短直角边长为a,较长直角边长为b,那么![]() 的值为 .
的值为 .
2、美国第二十届总统加菲尔德也曾经给出了勾股定理的一种证明方法,如图2所示,
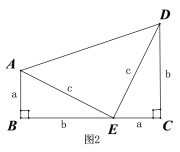
他用两个全等的直角三角形和一个等腰直角三角形拼出了一个直角梯形,请你利用此图形验证勾股定理.
证明:∵直角梯形ABCD的面积可以用两种方法表示:
第一种方法表示为:
第二种方法表示为:
∴ =
∴![]()
探索创新:
用纸做成四个全等的直角三角形,两直角边的长分别为a和b,斜边长为c,请你开动脑筋,将它们拼成一个能证明勾股定理的图形(不同于上面图1和图2).请画出你拼成的图形,并用你画的图形证明勾股定理.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为更好的了解中学生课外阅读的情况,学校团委将初一年级学生一学期阅读课外书籍量分为A(3本以内)、B(3——6本)、C(6——10本)、D(10本以上)四种情况进行了随机调查,并根据调查结果制成了如下两幅不完整的统计图.请结合统计图所给信息解答上列问题:
(1)在扇形统计图中C所占的百分比是多少?
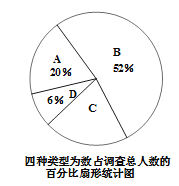
(2)请将折线统计图补充完整;

(3)学校团委欲从课外阅读量在10本以上的同学中随机邀请两位参加学校举办的“书香致远 墨卷至恒”主题读书日的形象大使,请你用列表法或画树状图的方法,求所选出的两位同学恰好都是女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 为更新果树品种,某果园计划新购进A、B两个品种的果树苗栽植培育,若计划购进这两种果树苗共45棵,其中A种苗的单价为7元/棵,购买B种苗所需费用y(元)与购买数量x(棵)之间存在如图所示的函数关系.
(1)求y与x的函数关系式;
(2)若在购买计划中,B种苗的数量不超过35棵,但不少于A种苗的数量,请设计购买方案,使总费用最低,并求出最低费用.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】赛龙舟是端午节的主要习俗,某市甲乙两支龙舟队在端午节期间进行划龙舟比赛,从起点A驶向终点B,在整个行程中,龙舟离开起点的距离y(米)与时间x(分钟)的对应关系如图所示,请结合图象解答下列问题:
(1)起点A与终点B之间相距多远?
(2)哪支龙舟队先出发?哪支龙舟队先到达终点?
(3)分别求甲、乙两支龙舟队的y与x函数关系式;
(4)甲龙舟队出发多长时间时两支龙舟队相距200米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在4×4的网格中存在线段AB,每格表示一个单位长度,并构建了平面直角坐标系.
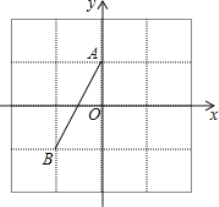
(1)直接写出点A、B的坐标:A( , ),B( , );
(2)请在图中确定点C(1,﹣2)的位置并连接AC、BC,则△ABC是 三角形(判断其形状);
(3)在现在的网格中(包括网格的边界)存在一点P,点P的横纵坐标为整数(在格点上),连接PA、PB后得到△PAB为等腰三角形,则满足条件的点P有 个.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com