
【题目】如图:在4×4的网格中存在线段AB,每格表示一个单位长度,并构建了平面直角坐标系.
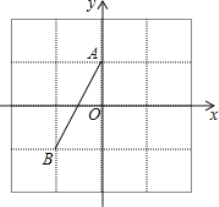
(1)直接写出点A、B的坐标:A( , ),B( , );
(2)请在图中确定点C(1,﹣2)的位置并连接AC、BC,则△ABC是 三角形(判断其形状);
(3)在现在的网格中(包括网格的边界)存在一点P,点P的横纵坐标为整数(在格点上),连接PA、PB后得到△PAB为等腰三角形,则满足条件的点P有 个.
科目:初中数学 来源: 题型:
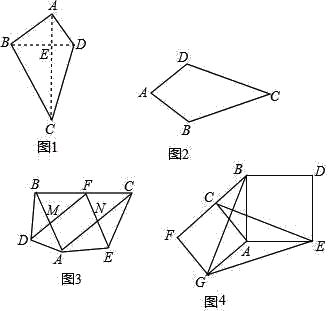
【题目】阅读理解:如图1,我们把对角线互相垂直的四边形叫做垂美四边形.垂美四边形有如下性质:
垂美四边形的两组对边的平方和相等.
已知:如图1,四边形ABCD是垂美四边形,对角线AC、BD相交于点E.
求证:AD2+BC2=AB2+CD2
证明:∵四边形ABCD是垂美四边形
∴AC⊥BD,
∴∠AED=∠AEB=∠BEC=∠CED=90°,
由勾股定理得,AD2+BC2=AE2+DE2+BE2+CE2,
AB2+CD2=AE2+BE2+CE2+DE2,
∴AD2+BC2=AB2+CD2.
拓展探究:
(1)如图2,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂美四边形吗?请说明理由.
(2)如图3,在Rt△ABC中,点F为斜边BC的中点,分别以AB,AC为底边,在Rt△ABC外部作等腰三角形ABD和等腰三角形ACE,连接FD,FE,分别交AB,AC于点M,N.试猜想四边形FMAN的形状,并说明理由;
问题解决:
如图4,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连接CE,BG,GE,已知AC=4,AB=5.求GE长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某市初三学生的体育测试成绩和课外体育锻炼时间的情况,现从全市初三学生体育测试成绩中随机抽取200名学生的体育测试成绩作为样本.体育成绩分为四个等次:优秀、良好、及格、不及格.
体育锻炼时间 | 人数 |
4≤x≤6 |
|
2≤x<4 | 43 |
0≤x<2 | 15 |
(1)试求样本扇形图中体育成绩“良好”所对扇形圆心角的度数;
(2)统计样本中体育成绩“优秀”和“良好”学生课外体育锻炼时间表(如图表所示),请将图表填写完整(记学生课外体育锻炼时间为x小时);
(3)全市初三学生中有14400人的体育测试成绩为“优秀”和“良好”,请估计这些学生中课外体育锻炼时间不少于4小时的学生人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C是线段AB上除点A、B外的任意一点,分别以AC、BC为边在线段AB的同旁作等边△ACD和等边△BCE,连接AE交DC于M,连接BD交CE于N,连接MN.
(1)求证:AE=BD;
(2)请判断△CMN的形状,并说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
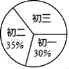
【题目】某初中在“读书共享月”活动中.学生都从家中带了图书到学校给大家共享阅读.经过抽样调查得知,初一人均带了2册;初二人均带了3.5册:初三人均带了2.5册.已知各年级学生人数的扇形统计图如图所示,其中初三共有210名学生.请根据以上信息解答下列问题:
(1)扇形统计图中,初三年级学生数所对应的圆心角为 °;
(2)该初中三个年级共有 名学生;
(3)估计全校学生人均约带了多少册书到学校?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:
①无理数都是无限小数;
②![]() 的算术平方根是3;
的算术平方根是3;
③数轴上的点与实数一一对应;
④平方根与立方根等于它本身的数是0和1;
⑤若点A(-2,3)与点B关于x轴对称,则点B的坐标是(-2,-3).
其中正确的个数是( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答下列各题:
(1)(﹣3.6)+(+2.5)
(2)-![]() ﹣(﹣3
﹣(﹣3![]() )﹣2
)﹣2![]() +
+![]()
(3)(﹣49)﹣(+91)﹣(﹣5)+(﹣9)
(4)﹣5﹣(﹣11)+2![]() ﹣(﹣
﹣(﹣![]() )
)
(5)3![]() ﹣(﹣
﹣(﹣![]() )+2
)+2![]() +(﹣
+(﹣![]() )
)
(6)![]() ﹣|﹣1
﹣|﹣1![]() |﹣(+2
|﹣(+2![]() )﹣(﹣2.75)
)﹣(﹣2.75)
(7)(﹣7)﹣(﹣11)+(﹣9)﹣(+2)
(8)(﹣4![]() )﹣(+5
)﹣(+5![]() )﹣(﹣4
)﹣(﹣4![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
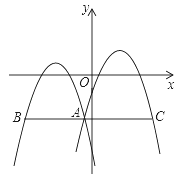
【题目】如图,在平面直角坐标系中,抛物线y=m(x+3)2+n与y=m(x﹣2)2+n+1交于点A.过点A作x轴的平行线,分别交两条抛物线于点B、C(点B在点C左侧),则线段BC的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,O是边AC上一点,以O为圆心,OA为半径的圆分别交AB,AC于点E,D,在BC的延长线上取点F,使得BF=EF,EF与AC交于点G.
(1)试判断直线EF与⊙O的位置关系,并说明理由;
(2)若OA=2,∠A=30°,求图中阴影部分的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com