练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

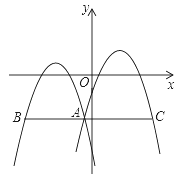
    【题目】如图，在平面直角坐标系中，抛物线y=m（x+3）2+n与y=m（x﹣2）2+n+1交于点A．过点A作x轴的平行线，分别交两条抛物线于点B、C（点B在点C左侧），则线段BC的长为_____．

    【答案】10

    【解析】

    设抛物线y=m（x+3）2+n的对称轴与线段BC交于点E，抛物线y=m（x﹣2）2+n+1的对称轴与线段BC交于点F，由抛物线的对称性结合BC═2（AE+AF），即可求出结论．

    设抛物线y=m（x+3）2+n的对称轴与线段BC交于点E，抛物线y=m（x﹣2）2+n+1的对称轴与线段BC交于点F，如图所示．

    由抛物线的对称性，可知：BE=AE，CF=AF，

    ∴BC=BE+AE+AF+CF=2（AE+AF）=2×[2-(-3)]=10．

    故答案为：10．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】赛龙舟是端午节的主要习俗，某市甲乙两支龙舟队在端午节期间进行划龙舟比赛，从起点A驶向终点B，在整个行程中，龙舟离开起点的距离y（米）与时间x（分钟）的对应关系如图所示，请结合图象解答下列问题：

    （1）起点A与终点B之间相距多远？

    （2）哪支龙舟队先出发？哪支龙舟队先到达终点？

    （3）分别求甲、乙两支龙舟队的y与x函数关系式；

    （4）甲龙舟队出发多长时间时两支龙舟队相距200米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图：在4×4的网格中存在线段AB，每格表示一个单位长度，并构建了平面直角坐标系．

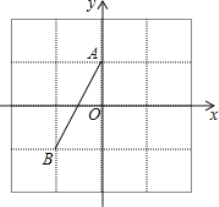
    （1）直接写出点A、B的坐标：A（　 　，　 　），B（　 　，　 　）；

    （2）请在图中确定点C（1，﹣2）的位置并连接AC、BC，则△ABC是　 　 三角形（判断其形状）；

    （3）在现在的网格中（包括网格的边界）存在一点P，点P的横纵坐标为整数（在格点上），连接PA、PB后得到△PAB为等腰三角形，则满足条件的点P有　 　个．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知Rt△ABC中，∠B=90°，

    （1）根据要求作图（尺规作图，保留作图痕迹，不写画法）：

    ①作∠BAC的平分线AD交BC于D；

    ②作线段AD的垂直平分线交AB于E，交AC于F，垂足为H；

    ③连接ED．

    （2）在（1）的基础上写出一对全等三角形：△　 　≌△　 　并加以证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在长方形ABCD中，AB=10厘米，BC=6厘米，点P沿AB边从点A开始向点B以3厘米/秒的速度移动；点Q沿DA边从点D开始向点A以2厘米/秒的速度移动.如果P、Q同时出发，用t (秒）表示移动的时间，那么：

    （1）如图1,用含t的代数式表示AP= ，AQ= .并求出当t为何值时线段AP=AQ.

    （2）如图2,在不考虑点P的情况下，连接QB，问：当t为何值时△QAB的面积等于长方形面积的.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

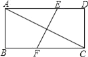
    【题目】如图，在矩形ABCD中，AB=2，AD=4，AC的垂直平分线EF交AD于点E、交BC于点F，则EF的长为（　　）

    A. 4 B. 2 C. D. 2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线y=﹣2x+7与x轴、y轴分别相交于点C、B，与直线y=x相交于点A．

    (1)求A点坐标；

    (2)求△OAC的面积；

    (3)如果在y轴上存在一点P，使△OAP是以OA为底边的等腰三角形，求P点坐标；

    (4)在直线y=﹣2x+7上是否存在点Q，使△OAQ的面积等于6？若存在，请求出Q点的坐标，若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】李老师为了了解学生暑期在家的阅读情况，随机调查了20名学生某一天的阅读小时数，具体情况统计如下：

    阅读时间

    （小时）

    2

    2.5

    3

    3.5

    4

    学生人数（名）

    1

    2

    8

    6

    3

    则关于这20名学生阅读小时数的说法正确的是（　　）

    A. 众数是8 B. 中位数是3 C. 平均数是3 D. 方差是0.34

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】自2008年实施国家知识产权战略以来，我国具有独立知识产权的发明专利日益增多．下图显示了2010﹣2013年我国发明专利申请量占世界发明专利申请量的比重．根据统计图提供的信息，下列说法不合理的是（　　）

    A. 统计图显示了2010﹣2013年我国发明专利申请量占世界发明专利申请量的比重的情况

    B. 我国发明专利申请量占世界发明专利申请量的比重，由2010年的19.7%上升至2013年的32.1%

    C. 2011年我国发明专利申请量占世界发明专利申请量的比重是28%

    D. 2010﹣2013年我国发明专利申请量占世界发明专利申请量的比重逐年增长

    查看答案和解析>>

    同步练习册答案