
【题目】如图,直线y=﹣2x+7与x轴、y轴分别相交于点C、B,与直线y=![]() x相交于点A.
x相交于点A.
(1)求A点坐标;
(2)求△OAC的面积;
(3)如果在y轴上存在一点P,使△OAP是以OA为底边的等腰三角形,求P点坐标;
(4)在直线y=﹣2x+7上是否存在点Q,使△OAQ的面积等于6?若存在,请求出Q点的坐标,若不存在,请说明理由.

【答案】(1)A点坐标是(2,3);(2)![]() =
=![]() ;(3)P点坐标是(0,
;(3)P点坐标是(0, ![]() );(4)点Q是坐标是(
);(4)点Q是坐标是(![]() ,
,![]() )或(
)或(![]() ,-
,-![]() ).
).
【解析】
解析
联立方程,解方程即可求得;
C点位直线y=﹣2x+7与x轴交点,可得C点坐标为(![]() ,0),由(1)得A点坐标,可得
,0),由(1)得A点坐标,可得![]() 的值;
的值;
(3)设P点坐标是(0,y),根据勾股定理列出方程,解方程即可求得;
(4)分两种情况:①当Q点在线段AB上:作QD⊥y轴于点D,则QD=x,根据
![]() =
=![]() -
-![]() 列出关于x的方程解方程求得即可;②当Q点在AC的延长线上时,作QD⊥x轴于点D,则QD=-y,根据
列出关于x的方程解方程求得即可;②当Q点在AC的延长线上时,作QD⊥x轴于点D,则QD=-y,根据![]() =
=![]() -
- ![]() 列出关于y的方程解方程求得即可.
列出关于y的方程解方程求得即可.
解(1)解方程组: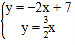 得:
得:![]() ,
,
![]() A点坐标是(2,3);
A点坐标是(2,3);
(2)![]() C点位直线y=﹣2x+7与x轴交点,可得C点坐标为(
C点位直线y=﹣2x+7与x轴交点,可得C点坐标为(![]() ,0)
,0)
![]()
![]() =
=![]() =
=![]()
(3)设P点坐标是(0,y ),
![]() △OAP是以OA为底边的等腰三角形,
△OAP是以OA为底边的等腰三角形,
![]() OP=PA,
OP=PA,
![]()
![]() ,
,
解得y=![]() ,
,
![]() P点坐标是(0,
P点坐标是(0, ![]() ),
),
故答案为(0, ![]() );
);
(4)存在;
由直线y=-2x+7可知B(0,7),C(![]() ,0),
,0),
![]()
![]() =
=![]() =
=![]() <6,
<6,
![]() =
=![]() =7>6,
=7>6,
![]() Q点有两个位置:Q在线段AB上和AC的延长线上,设点Q的坐标是(x,y),
Q点有两个位置:Q在线段AB上和AC的延长线上,设点Q的坐标是(x,y),
当Q点在线段AB上:作QD⊥y轴于点D,如图1, 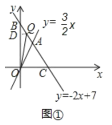
则QD=x,![]()
![]() =
=![]() -
-![]() =7-6=1,
=7-6=1,
![]()
![]() OB
OB![]() QD=1,即:
QD=1,即: ![]()
![]() 7x=1,
7x=1,
![]() x=
x=![]() ,
,
把x=![]() 代入y=-2x+7,得y=
代入y=-2x+7,得y=![]() ,
,
![]() Q的坐标是(
Q的坐标是(![]() ,
,![]() ),
),
当Q点在AC的延长线上时,作QD⊥x轴于点D,如图2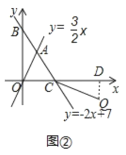
则QD=-y,
![]()
![]() =
=![]() -
- ![]() =6-
=6-![]() =
=![]() ,
,
![]()
![]() OC
OC![]() QD=
QD=![]() ,即:
,即:![]() ,
,
![]() y=-
y=-![]() ,
,
把y=-![]() 代入y=-2x+7,解得x=
代入y=-2x+7,解得x=![]()
![]() Q的坐标是(
Q的坐标是(![]() ,-
,-![]() ),
),
综上所述:点Q是坐标是(![]() ,
,![]() )或(
)或(![]() ,-
,-![]() ).
).


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:初中数学 来源: 题型:
【题目】一次函数![]() 的图象经过点(-3,-2).
的图象经过点(-3,-2).
(1)求这个函数表达式;
(2)判断(-5,3)是否在这个函数的图象上.
(3)点M在直线y=kx+4上且到y轴的距离是3,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
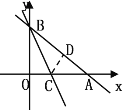
【题目】如图,一次函数的图像与x轴、y轴分别交于A、B两点,且A、B的坐标分别为(4,0),(0,3).
(1)求一次函数的表达式.
(2)点C在线段OA上,沿BC将△OBC翻折,O点恰好落在AB上的D处,
求直线BC的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小张骑车往返于甲、乙两地,距甲地的路程y(千米)与时间x(时)的函数图象如图所示.
(1)小张在路上停留 小时,他从乙地返回时骑车的速度为 千米/时;
(2)小王与小张同时出发,按相同路线匀速前往乙地,距甲地的路程y(千米)与时间x(时)的函数关系式为y=10x+10.请作出此函数图象,并利用图象回答:小王与小张在途中共相遇 次;
(3)请你计算第三次相遇的时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
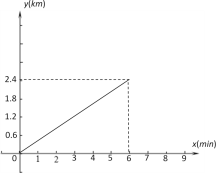
【题目】已知A、B两地相距2.4km,甲骑车匀速从A地前往B地,如图表示甲骑车过程中离A地的路程y(km)与他行驶所用的时间x(min)之间的关系.根据图像解答下列问题:
(1)甲骑车的速度是 km/min;
(2)若在甲出发时,乙在甲前方0.6km处,两人均沿同一路线同时出发匀速前往B地,在第3分钟甲追上了乙,两人到达B地后停止.请在下面同一平面直角坐标系中画出乙离A地的距离y乙(km)与所用时间x(min)的关系的大致图像;
(3)乙在第几分钟到达B地?
(4)两人在整个行驶过程中,何时相距0.2km?
查看答案和解析>>
科目:初中数学 来源: 题型:
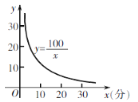
【题目】去学校食堂就餐,经常会在一个买菜窗口前等待. 经调查发现,同学的舒适度指数y与等待时间x(分)之间存在如下的关系:y=![]() ,求:
,求:
(1)若等待时间x=5分钟时,求舒适度y的值;
(2)舒适度指数不低于10时,同学才会感到舒适.函数y=![]() (x>0)的图象如图,请根据图象说明,作为食堂的管理员,让每个在窗口买菜的同学最多等待多少时间?
(x>0)的图象如图,请根据图象说明,作为食堂的管理员,让每个在窗口买菜的同学最多等待多少时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,AB是⊙O的直径,点P在CA的延长线上,∠CAD=45°.
(Ⅰ)若AB=4,求 ![]() 的长;
的长;
(Ⅱ)若 ![]() =
= ![]() ,AD=AP,求证:PD是⊙O的切线.
,AD=AP,求证:PD是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠BOC=60°,OF平分∠BOC.若AO⊥BO,OE平分∠AOC,则∠EOF的度数是( )
A. 45°
B. 15°
C. 30°或60°
D. 45°或15°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com